nombre égal à un carré plus k fois un carré

NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 22/09/2021 Orientation générale DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Nombres
Débutants Addition	Variations sur les carrés et les cubes				Glossaire Addition
INDEX PARTITION CARRÉS	Carrés	Chiffres répétés	Repdigits	Chiffres consécutifs
	Produits	66 x 67 …	66 x 99 …	Factorisation
	Sommes	Somme double	A² + kB²	Factorisation – Algorithme
	Différences	Propriétés	Écart 1, 2, …	Trouver la dif. des carrés
	Autres	Table 1 à 100	Repdigits	Table des Repdigits
		Curiosités	Tableau synthèse	a² – b² = c² – d²
		Chiffres	Concaténation
	Sommaire de cette page >>> Approche – Le nombre 3 600 >>> Records sans ordre >>> Records AVEC ordre >>> Records AVEC ordre avec le CARRÉS >>> Propriété >>> Liste de nombres en a²+ kb²

NOMBRE = a² + k·b²

Nombres tels que n = a² + kb². Ils sont très nombreux.On cherche ceux pour k continu de 1 à kmax. Ou encore, la même propriété mais pour les carrés seulement.

On sait que tout nombre est la somme de quatre carrés (théorème de Lagrange). Certains sont somme de deux ou trois carrés >>>

Approche – Le nombre 3 600

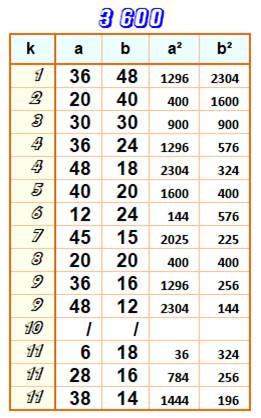
Le nombre 3 600 est un carré (60²).

Il est multi-somme de carrés de la forme:
a + kb² pour k continu de 1 à 9.

C'est un record pour un carré >>>

Le tableau se poursuit après 11.

Voir Nombre 3 600

Records sans ordre
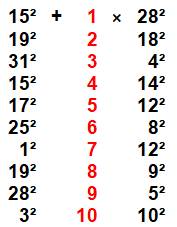
Exemple avec 17 Record avec 4 représentations jusqu'à k = 10. Le nombre suivant est 73 avec 7 représentations.	Les quatre présentations pour 17
Nombre suivi de k 2, {1} 17, {1, 2, 4, 8} 73, {1, 2, 3, 4, 6, 8, 9} 97, {1, 2, 3, 4, 6, 8, 9} 241, {1, 2, 3, 4, 5, 6, 8, 9, 10} 409, {1, 2, 3, 4, 5, 6, 8, 9, 10} 1009, {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}	Nombre suivi de k puis doublets [a, b] 2, {1}, [[1, 1]] 17, {1, 2, 4, 8}, [[1, 4], [3, 2], [1, 2], [3, 1]] 73, {1, 2, 3, 4, 6, 8, 9}, [[3, 8], [1, 6], [5, 4], [3, 4], [7, 2], [1, 3], [8, 1]] 97, {1, 2, 3, 4, 6, 8, 9}, [[4, 9], [5, 6], [7, 4], [9, 2], [1, 4], [5, 3], [4, 3]] 241, {1, 2, 3, 4, 5, 6, 8, 9, 10}, [[4, 15], [13, 6], [7, 8], [15, 2], [14, 3], [5, 6], [13, 3], [4, 5], [9, 4]] 409, {1, 2, 3, 4, 5, 6, 8, 9, 10}, [[3, 20], [11, 12], [19, 4], [3, 10], [2, 9], [5, 8], [11, 6], [20, 1], [7, 6]] 1009, {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, [[15, 28], [19, 18], [31, 4], [15, 14], [17, 12], [25, 8], [1, 12], [19, 9], [28, 5], [3, 10]]

Voir Nombre 17 / Nombre 73 / Nombre 1009

Records AVEC ordre
Exemple avec 17 Record avec 2 représentations consécutives k = 1 et k = 2. Le nombre suivant est 73 avec 4 représentations consécutives.	Les dix présentations consécutives pour 1009
Nombre suivi de k 2, {1} 17, {1, 2, 4, 8} 73, {1, 2, 3, 4, 6, 8, 9} 97, {1, 2, 3, 4, 6, 8, 9} 241, {1, 2, 3, 4, 5, 6, 8, 9, 10} 409, {1, 2, 3, 4, 5, 6, 8, 9, 10} 1009, {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}	Nombre suivi de k puis doublets [a, b] 2, {1}, [[1, 1]] 17, {1, 2, 4, 8}, [[1, 4], [3, 2], [1, 2], [3, 1]] 73, {1, 2, 3, 4, 6, 8, 9}, [[3, 8], [1, 6], [5, 4], [3, 4], [7, 2], [1, 3], [8, 1]] 97, {1, 2, 3, 4, 6, 8, 9}, [[4, 9], [9, 4], [5, 6], [7, 4], [9, 2], [1, 4], [5, 3], [4, 3]] 241, {1, 2, 3, 4, 5, 6, 8, 9, 10}, [[4, 15], [13, 6], [7, 8], [15, 2], [14, 3], [5, 6], [13, 3], [4, 5], [9, 4]] 409, {1, 2, 3, 4, 5, 6, 8, 9, 10}, [[3, 20], [11, 12], [19, 4], [3, 10], [2, 9], [5, 8], [11, 6], [20, 1], [7, 6]] 1009, {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, [[15, 28], [19, 18], [31, 4], [15, 14], [17, 12], [25, 8], [1, 12], [19, 9], [28, 5], [3, 10]]

Records AVEC ordre avec le CARRÉS
Exemple avec 225 = 15² Record avec 2 représentations consécutives k = 1 et k = 2. Le nombre suivant est 900 = 30² avec 6 représentations consécutives.		Les deux présentations consécutives pour 225 225 = 9² + 12² 225 = 5² + 2x 10² Pour ce nombre, on trouve également une égalité pour k = 4, 5, 6, 8, 9 … Mais le k = 3 est manquant.
Nombre, son carré suivi de k puis doublets [a, b] Présentations pour k de 1 à 20.	5, 25, {1, 4, 6, 9, 16}, [[3, 4], [3, 2], [1, 2], [4, 1], [3, 1]] 15, 225, {1, 2, 4, 5, 6, 8, 9, 11, 14, 16}, [[9, 12], [5, 10], [9, 6], [10, 5], [3, 6], [5, 5], [9, 4], [12, 3], [7, 4], [1, 4], [13, 2], [9, 3]] 30, 900, {1, 2, 3, 4, 5, 6, 8, 9, 11, 14, 16, 19, 20}, [[18, 24], [10, 20], [15, 15], [18, 12], [24, 9], [20, 10], [6, 12], [10, 10], [18, 8], [24, 6], [3, 9], [14, 8], [19, 7], [25, 5], [2, 8], [26, 4], [18, 6], [27, 3], [20, 5]] 34, 1156, {1, 2, 3, 4, 8, 9, 13, 15, 16, 18, 19}, [[16, 30], [2, 24], [17, 17], [16, 15], [30, 8], [2, 12], [16, 10], [18, 8], [14, 8], [30, 4], [2, 8], [15, 7]] 39, 1521, {1, 2, 3, 4, 5, 8, 9, 10, 12, 14, 16, 17}, [[15, 36], [13, 26], [33, 12], [15, 18], [26, 13], [13, 13], [15, 12], [36, 5], [9, 12], [33, 6], [11, 10], [25, 8], [15, 9], [12, 9]] 60, 3600, {1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 12, 14, 15, 16, 19, 20}, [[36, 48], [20, 40], [30, 30], [36, 24], [48, 18], [40, 20], [12, 24], [45, 15], [20, 20], [36, 16], [48, 12], [6, 18], [28, 16], [38, 14], [50, 10], [30, 15], [4, 16], [52, 8], [15, 15], [36, 12], [48, 9], [54, 6], [40, 10]] 120, 14400, {1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 12, 14, 15, 16, 19, 20}, [[72, 96], [96, 72], [40, 80], [60, 60], [72, 48], [96, 36], [80, 40], [24, 48], [15, 45], [90, 30], [40, 40], [72, 32], [96, 24], [12, 36], [56, 32], [76, 28], [100, 20], [60, 30], [8, 32], [104, 16], [30, 30], [105, 15], [72, 24], [96, 18], [108, 12], [80, 20]] 174, 30276, {1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 13, 16, 20}, [[120, 126], [126, 120], [58, 116], [87, 87], [120, 63], [126, 60], [66, 72], [76, 70], [116, 58], [164, 26], [150, 36], [162, 24], [58, 58], [120, 42], [126, 40], [145, 29], [18, 48], [126, 30], [66, 36], [76, 35], [116, 29], [164, 13]] 180, 32400, {1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 12, 14, 15, 16, 17, 18, 19, 20}, [[108, 144], [144, 108], [60, 120], [140, 80], [90, 90], [108, 72], [144, 54], [20, 80], [120, 60], [36, 72], [135, 45], [60, 60], [140, 40], [108, 48], [144, 36], [18, 54], [70, 50], [84, 48], [114, 42], [150, 30], [158, 26], [172, 16], [90, 45], [12, 48], [100, 40], [156, 24], [45, 45], [108, 36], [144, 27], [160, 20], [60, 40], [162, 18], [20, 40], [120, 30]]

Propriété – Énoncée par V. Raman

Si un nombre composé C peut s'écrire sous la forme C = a² + kb² pour a et b entiers, alors tout nombre premier p avec C élevé à une puissance impaire peut s'écreise sous la forme P = c² + kd² pour c et d entiers.

Ceci est valable pour k = 1, 2, 3. Vrai aussi pour k = 7 à l'exception de p = 2.

If a composite number C, say, can be written in the form C = a^2+k*b^2, for some integers a & b, then every prime factor P (for C) being raised to an odd power can be written in the form P = c^2+k*d^2, for some integers c & d.

This statement is only true for k = 1, 2, 3.

For k = 7, with the exception of the prime factor 2, the statement mentioned above is true.

Voir OEIS A216682

Liste de nombres en a²+ kb²

a² + b²

a² + 2b²

17, 1, 4, 3, 2 => 17 = 1² + 4² = 3² 2x2²

18, 3, 3, 4, 1

34, 3, 5, 4, 3

41, 4, 5, 3, 4

68, 2, 8, 6, 4

72, 6, 6, 8, 2

73, 3, 8, 1, 6

82, 1, 9, 8, 3

89, 5, 8, 9, 2

97, 4, 9, 5, 6

17, 18, 34, 34, 41, 41, 68, 68, 72, 73, 73, 82, 82, 89, 89, 97, 97, 113, 113, 136, 136, 137, 137, 146, 146, 153, 153, 153, 153, 153, 153, 162, 162, 164, 164, 178, 178, 193, 193, 194, 194, 225, 225, 226, 226, 233, 233, 241, 241, 242, 257, 257, 272, 272, 274, 274, 281, 281, 288, 289, 289, 292, 292, 306, 306, 306, 306, 306, 306, 313, 313, 328, 328, 337, 337, 353, 353, 356, 356, 369, 369, 369, 369, 369, 369, 386, 386, 388, 388, 401, 401, 409, 409, 425, 425, 425, 425, 425, 425, 433, 433, 449, 449, 450, 450, 450, 452, 452, 457, 457, 466, 466, 482, 482, 514, 514, 521, 521, 544, 544, 548, 548, 562, 562, 569, 569, 577, 577, 578, 578, 578, 584, 584, 593, 593, 601, 601, 612, 612, 612, 612, 612, 612, 617, 617, 626, 626, 641, 641, 648, 648, 656, 656, 657, 657, 657, 657, 657, 657, 673, 673, 674, 674, 697, 697, 697, 697, 697, 697, 697, 697, 706, 706, 712, 712, 722, 738, 738, 738, 738, 738, 738, 761, 761, 769, 769, 772, 772, 776, 776, 801, 801, 801, 801, 801, 801, 802, 802, 809, 809, 818, 818, 833, 833, 850, 850, 850, 850, 850, 850, 857, 857, 866, 866, 873, 873, 873, 873, 873, 873, 881, 881, 882, 898, 898, 900, 900, 904, 904, 914, 914, 929, 929, 932, 932, 937, 937, 953, 953, 964, 964, 968, 977, 977 …

a² + b²

a² + 2b²

a² + 3b²

73, 3, 8, 1, 6, 5, 4 = > 73 = 3² + 8² = 1² + 2x6² = 5² + 3x4²

97, 4, 9, 5, 6, 7, 4

193, 7, 12, 11, 6, 1, 8

241, 4, 15, 13, 6, 7, 8

292, 6, 16, 2, 12, 7, 9

292, 6, 16, 2, 12, 10, 8

292, 6, 16, 2, 12, 17, 1

193, 241, 292, 313, 337, 388, 409, 433, 457, 577, 601, 657, 673, 769, 772, 873, 900, 937, 964, 1009, 1033, 1129, 1153, 1156, 1168, 1201, 1249, 1252, 1297, 1321, 1348, 1489, 1521, 1552, 1609, 1636, 1657, 1732, 1737, 1753, 1777, 1801, 1825, 1828, 1873, 1993 …

a² + b²

a² + 2b²

a² + 3b²

a² + 4b²

73, 3, 8, 1, 6, 5, 4

97, 4, 9, 5, 6, 7, 4

193, 7, 12, 11, 6, 1, 8, 7, 6

241, 4, 15, 13, 6, 7, 8, 15, 2

292, 6, 16, 2, 12, 7, 9, 6, 8

292, 6, 16, 2, 12, 7, 9, 16, 3

292, 6, 16, 2, 12, 10, 8, 6, 8

292, 6, 16, 2, 12, 10, 8, 16, 3

292, 6, 16, 2, 12, 17, 1, 6, 8

292, 6, 16, 2, 12, 17, 1, 16, 3

313, 12, 13, 5, 12, 11, 8, 13, 6

337, 9, 16, 7, 12, 17, 4, 9, 8

73, 97, 193, 241, 292, 313, 337, 388, 409, 433, 457, 577, 601, 657, 673, 769, 772, 873, 900, 937, 964, 1009, 1033, 1129, 1153, 1156, 1168, 1201, 1249, 1252, 1297, 1321, 1348, 1489, 1521, 1552, 1609, 1636, 1657, 1732, 1737, 1753, 1777, 1801, 1825, 1828, 1873, 1993 …

a² + b²

a² + 2b²

a² + 3b²

a² + 5b²

241, 4, 15, 13, 6, 7, 8, 14, 3

409, 3, 20, 11, 12, 19, 4, 2, 9

601, 5, 24, 23, 6, 13, 12, 14, 9

769, 12, 25, 11, 18, 1, 16, 7, 12

900, 18, 24, 10, 20, 15, 15, 20, 10

241, 409, 601, 769, 900, 964, 1009, 1129, 1201, 1249, 1321, 1489, 1521, 1609, 1636, 1801, 2089, 2161, 2169, 2281, 2404, 2521, 2689, 3001, 3049, 3076, 3121, 3169, 3361, 3529, 3600, 3681, 3769, 3856, 3889, 4036, 4129, 4201, 4441, 4516, 4561, 4729, 4801, 4804, 4969, 4996, 5209, 5281, 5284, 5409 …

a² + b²

a² + 2b²

a² + 3b²

a² + 6b²

73, 3, 8, 1, 6, 5, 4

97, 4, 9, 5, 6, 7, 4

193, 7, 12, 11, 6, 1, 8, 13, 2

241, 4, 15, 13, 6, 7, 8, 5, 6

292, 6, 16, 2, 12, 7, 9, 14, 4

292, 6, 16, 2, 12, 10, 8, 14, 4

292, 6, 16, 2, 12, 17, 1, 14, 4

313, 12, 13, 5, 12, 11, 8, 17, 2

337, 9, 16, 7, 12, 17, 4, 11, 6

388, 8, 18, 10, 12, 5, 11, 2, 8

388, 8, 18, 10, 12, 14, 8, 2, 8

388, 8, 18, 10, 12, 19, 3, 2, 8

73, 97, 193, 241, 292, 313, 337, 388, 409, 433, 457, 577, 601, 657, 673, 769, 772, 873, 900, 937, 964, 1009, 1033, 1129, 1153, 1168, 1201, 1249, 1252, 1297, 1321, 1348, 1489, 1552, 1609, 1636, 1657, 1732, 1737, 1753, 1777, 1801, 1825, 1828, 1873, 1993, 2017, 2089, 2113, 2137, 2161, 2169, 2281, 2308, 2377, 2404, 2425, 2473, 2521 …

a² + b²

a² + 2b²

a² + 3b²

a² + 7b²

193, 7, 12, 11, 6, 1, 8, 9, 4

337, 9, 16, 7, 12, 17, 4, 15, 4

457, 4, 21, 13, 12, 5, 12, 3, 8

673, 12, 23, 5, 18, 25, 4, 15, 8

772, 14, 24, 22, 12, 2, 16, 18, 8

772, 14, 24, 22, 12, 23, 9, 18, 8

772, 14, 24, 22, 12, 25, 7, 18, 8

193, 337, 457, 673, 772, 1009, 1033, 1129, 1201, 1297, 1348, 1737, 1801, 1828, 1873, 2017, 2137, 2377, 2473, 2521, 2689, 2692, 2713, 2857, 3033, 3049, 3088, 3217, 3313, 3361, 3529, 3600, 3697, 3889, 4036, 4057, 4113, 4132, 4153, 4201, 4516, 4561, 4624, 4657, 4729, 4804, 4825, 4993, 5188, 5209, 5233, 5392, 5569, 5737, 5881, 6057, 6073, 6217, 6337, 6553, 6577, 6673, 6841, 6948, 7057, 7177, 7204, 7312, 7393, 7417, 7492, 7561, 7681, 7753, 8017, 8068, 8089, 8233, 8353, 8425, 8521, 8548, 8689, 8737, 8761, 8929, 9081, 9241, 9297, 9433, 9457, 9508, 9601, 9697, 9769, 9892 …

Dans ce cas, selon V. Raman

SSI = si et seulement si; Fi = facteurs du nombre

Suite	Carrés ne comportant que deux chiffres Chiffres répétés dans les carrés et les cubes Carrés et concaténation Carrés et repdigits Nombres doublement carré Puissance concaténation de n puissances S'y retrouver
Voir	Addition - Glossaire Addition des carrés Addition des entiers Addition des puissances Carrés magiques Conjecture de Goldbach Demlo (Nombres -) Nombres consécutifs Identités remarquables Impairs Palindromes Repdigit Répétition de motifs
Site	OEIS A216451 - Numbers which are simultaneously of the form x^2+y^2, x^2+2y^2, x^2+3y^2, x^2+7y^2, all with x>0, y>0 OEIS A216682 - Perfect squares which can be written in all the four forms a^2+b^2, a^2+2b^2, a^2+3b^2 and a^2+7*b^2, with a > 0 and b > 0
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Addition/P100a500/CarreAkB.htm