f NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 26/07/2014 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique
	Itérations
Débutants Général	Motifs				Glossaire Général
INDEX Motifs Magie	Pépites	66 x 67	66 x 99	Carrés
		Sommaire de cette page >>> Produit 3 x 4 >>> Produit 6 x 7 >>> Produit 9 x 10 >>> Produit 1 x 2 >>> Formation des produits pour 1 x 2 >>> Formation des produits pour 6 x 7

Motifs répétitifs

Produit d'un nombre et de son successeur

Exemple: 6 x 7 = 42 66 67 4422 666 667 444222 etc.

Produits itératifs 3 x 4; 3 x 5; 3 x 6 … 6 x 7; 6 x 9; 6 x 10 … 9 x 10; 9 x 11; 9 x 12 …

Ci-dessous, en fond jaune, les motifs parfaitement itératifs

3 x 4

1 => 3 x 4 = 12 2 33 34 1122 3 333 334 111222 4 3333 3334 11112222 5 33333 33334 1111122222 6 333333 333334 111111222222 7 3333333 3333334 11111112222222 8 33333333 33333334 1111111122222222 9 333333333 333333334 111111111222222222 10 3333333333 3333333334 11111111112222222222 Etc. Le motif se poursuit avec autant de 4 et de 2 que de 6 dans le nombre initial. Un autre motif avec 34 Suite Carrés en croissance cristalline

Autour de 3 x 4
3 x 2 = 6 33 x 32 = 1056 333 x 332 = 110556 3333 x 3332 = 11105556 33333 x 33332 = 1111055556	3 x 3 = 9 33 x 33 = 1089 333 x 333 = 110889 3333 x 3333 = 11108889 33333 x 33333 = 1111088889
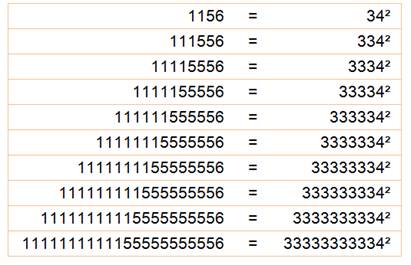
3 x 5 = 15 33 x 35 = 1155 333 x 335 = 111555 3333 x 3335 = 11115555 33333 x 33335 = 1111155555	3 x 6 = 18 33 x 36 = 1188 333 x 336 = 111888 3333 x 3336 = 11118888 33333 x 33336 = 1111188888 Ensuite, par exemple pour 3 x 7: 33333 x 33337 = 1111222221

Voir Carré des repdigits

6 x 7

1 => 6 x 7 = 42 2 66 67 4422 3 666 667 444222 4 6666 6667 44442222 5 66666 66667 4444422222 6 666666 666667 444444222222 7 6666666 6666667 44444442222222 8 66666666 66666667 4444444422222222 9 666666666 666666667 444444444222222222 10 6666666666 6666666667 44444444442222222222 11 66666666666 66666666667 4444444444422222222222 12 666666666666 666666666667 444444444444222222222222 Etc. Le motif se poursuit avec autant de 4 et de 2 que de 6 dans le nombre initial.

Autour de 6 x 7
6 x 5 = 30 66 x 65 = 4290 666 x 665 = 442890 6666 x 6665 = 44428890 66666 x 66665 = 4444288890	6 x 6 = 36 66 x 66 = 4356 666 x 666 = 443556 6666 x 6666 = 44435556 66666 x 66666 = 4444355556
6 x 8 = 48 66 x 68 = 4488 666 x 668 = 444888 6666 x 6668 = 44448888 66666 x 66668 = 4444488888	6 x 9 = 54 66 x 69 = 4554 666 x 669 = 445554 6666 x 6669 = 44455554 66666 x 66669 = 4444555554 Le motif est itératif mais avec une coquetterie pour les unités
Notez le motif itératif sur la base du carré de 65: 65 x 65 = 4225 665 x 665 = 442225 6665 x 6665 = 44422225 66665 x 66665 = 4444222225 666665 x 666665 = 444442222225 6666665 x 6666665 = 44444422222225 66666665 x 66666665 = 4444444222222225 666666665 x 666666665 = 444444442222222225 6666666665 x 6666666665 = 44444444422222222225 Voir Explications du produit 6x 7

9 x 10
1 => 9 x 10 = 90 2 99 100 9900 3 999 1000 999000 4 9999 10000 99990000 5 99999 100000 9999900000 Etc. Résultat qui paraît plus évident que ci-dessus!

Autour de 9 x 10
9 x 8 = 72 99 x 98 = 9702 999 x 998 = 997002 9999 x 9998 = 99970002 99999 x 99998 = 9999700002	9 x 9 = 81 99 x 99 = 9801 999 x 999 = 998001 9999 x 9999 = 99980001 99999 x 99999 = 9999800001
9 x 11 = 99 99 x 101 = 9999 999 x 1001 = 999999 9999 x 10001 = 99999999 99999 x 100001 = 9999999999	9 x 12 = 108 99 x 102 = 10098 999 x 1002 = 1000998 9999 x 10002 = 100009998 99999 x 100002 = 10000099998

1 x 2
Motif semi-régulier. Le 5 est le premier à dérailler pour la progression à gauche 12346 au lieu de 12345. Croissance à droite Il est logique que les (n – 1) derniers chiffres du résultat soient ceux du résultat précédent. En effet par exemple: 11 x 12 = 132 on doit retrouver 32 dans le résultat suivant. Or 111 x 112 = (100 + 11)(100 + 12) = 100x100 + 11x100 + 12x100 + 11x 12 = 12400 + 132 Les deux 0 finaux laissent se matérialiser les deux chiffres finaux du produit précédent. Croissance à gauche Moins évident à percevoir. Par exemple: 111 x 112 = (110 + 1)(110 + 2) = 12100 + 110 + 220 + 2 Tout seul l'exemple ne permet pas d'imaginer la croissance à gauche. Voyons la progression du produit en montrant les résultats intermédiaires:
11x 12 = 100 + 20 + 10 + 2 = 132	111x 112 = + 12100 + 220 + 110 + 2 = 12432	1111x 1112 = + 1232100 + 2220 + 1110 + 2 = 1235432	11111x 11112 = + 123432100 + 22220 + 11110 + 2 = 123465432	111111x 111112 = + 12345432100 + 222220 + 111110 + 2 = 12345765432
La progression du premier nombre (en haut) croit comme le carré du nombre initial alors que les deux du milieu sont du même ordre de grandeur que le nombre initial laissant la place aux chiffres de gauche du nombre d'en haut.

Quelques autres
5 x 6 = 30 55 x 56 = 3080 555 x 556 = 308580 5555 x 5556 = 30863580 55555 x 55556 = 3086413580 555555 x 555556 = 308641913580 5555555 x 5555556 = 30864196913580	8 x 10 = 80 88 x 90 = 7920 888 x 890 = 790320 8888 x 8890 = 79014320 88888 x 88890 = 7901254320 888888 x 888890 = 790123654320 8888888 x 8888890 = 79012347654320

6 x 7 – Formation des produits
Sur le même modèle que pour le produit 1 x 2 nous allons examiner la progression des produits basés sur 6 x 7. 66 x 67 = (65 + 1)(65 + 2) = 65² + 3x65 + 2 = 4225 + 195 + 2 = 4422
66 x 67= 4225 + 195 + 2 = 4422	666 x 667= 442225 + 1995 + 2 = 444222	6666 x 6667= 44422225 + 19995 + 2 = 44442222	66666 x 66667= 4444222225 + 199995 + 2 = 4444422222	666666 x 666667= 444442222225 + 1999995 + 2 = 444444222222
Surprenante conjonction des nombres à additionner qui se reproduit sans fin. Il possible de faire le même raisonnement avec 66² = 4356. Par exemple: 666 x 667 = 666 (666 + 1) = 443556 + 666 = 444222. Le motif itératif est tout aussi visible.

Suite	Motif itératif sur 66 x 99 Magie avec les nombres
Voir	Chiffres – Glossaire Nombres à motif – Index Nombres et jeux Nombres pour débutants Pépites
Diconombre	Nombre 12 Nombre 34 Nombre 42
Livre	Maths – La petite encyclopédie collège – André Deledicq – Éditions de la Cité – 2004 (impression 2007)
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Iteration/aMOTIF/Mul6x7.htm