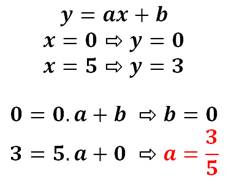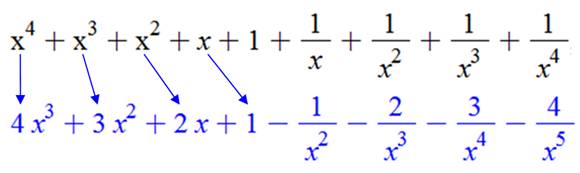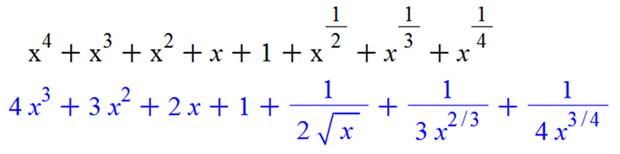NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 27/12/2018 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique Brèves de Maths
	ANALYSE
Débutants Général	Dérivées			Glossaire Dérivée
INDEX Analyse	Approche	Débutants	Développement
	Ficelles de première	Approche en première	Les dérivées usuelles
	Historique	Exemples résolus	Exemples (limites)
	Première	Sommaire de cette page >>> Prime et prime >>> Tangente >>> Pente et coefficient directeur >>> Dérivée >>> Dérivée et intégrale >>> Exemple de calcul

DÉRIVÉES – En classe de première

Quelques ficelles, trucs, notions pour bien démarrer en première. Les pièges … Un tour d'horizon.

Cette page a été construite suite à des échanges avec des élèves de première

Il y a PRIME & PRIME
Le prof parle de f et de f' (f prime). Je n'y comprends rien. C'est quoi ce f prime? Je sens bien que cela cache une nouvelle notion. Effectivement, vous avez été habitués en géométrie à noter en "prime" un point (ou un objet) du même type mais distinct. Comme ici sur le cercle: soit M un point du cercle et M' (M prime) un autre point sur le cercle. Avec les fonctions, le "prime" désigne de toutes nouvelles fonctions qui sont "dérivées" des premières. Pour visualiser tout de suite: ces nouvelles fonctions vont caractériser l'enveloppe de la courbe représentative de la fonction originelle. Cette "enveloppe" est constituée de toutes les droites tangentes à la courbe. Ces tangentes (droites bleues) caractérisent l'évolution de la courbe tangente en chaque point. Intuitivement, on peut dire: la courbe "monte" vite, moins vite; elle s'arrête pour repartir en descendant de plus en plus vite … Les droites tangentes montrent cette tendance, ces accroissements en plus et en moins.	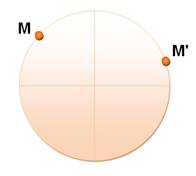En géométrie M et M' sont deux objets (points) de même nature. 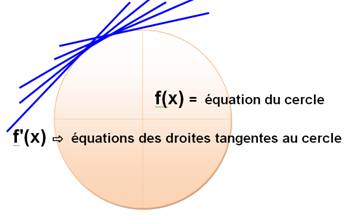En algèbre / analyse f(x) et f'(x) sont deux fonctions différentes. La seconde "enveloppe" la première.

Tangente
J'ai étudié la tangente d'un angle en trigonométrie; il y a la tangente en géométrie; et, ici, on reparle de tangente. Je sens la confusion me gagner... En trigonométrie la tangente d'un angle dans un triangle rectangle est égale au rapport (des longueurs) du côté opposé sur le côté adjacent. En langage imagé: "de combien je monte pour combien j'avance". La tangente caractérise donc une pente. En géométrie, la tangente en un point est la droite qui lèche la courbe en ce point sans la couper plusieurs fois. La tangente contient l'infiniment petit morceau de courbe autour du point de tangence (angle nul entre les deux). Sur une courbe, il y a une infinité de droites tangentes, autant que de points sur la courbe.	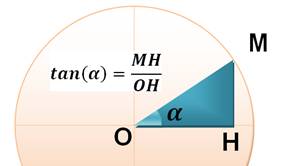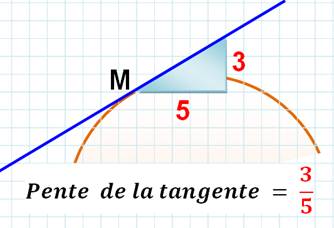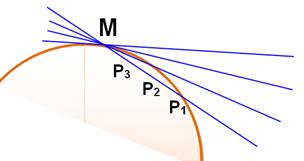En trigonométrie La tangente témoigne de la pente (angle alpha) de l'hypoténuse dans le triangle rectangle. En géométrie Les sécantes MPi coupent la courbe en des points de plus en plus rapprochés de M. Lorsque P est infiniment proche de M, la droite MP est la tangente en M à la courbe.

Voir Tangente en trigo.

Pente et coefficient directeur
Comment chiffrer l'inclinaison de la droite tangente en un point d'une courbe? En donnant l'accroissement de y pour une quantité donnée de progression en x. L'exemple donne 3 en y pour 5 en x. On est libre de choisir la taille du triangle rectangle. Si possible, on en prendra un qui tombe juste par rapport au quadrillage. Quel que soit celui choisi, le rapport sera toujours le même (homothétie). Faisons passer une repère (M, x , y) par le point M et nous serons armé pour donner l'équation de la droite tangente en M. Résolution: Le coefficient a de x est appelé le coefficient directeur de la droite; c'est aussi la pente de la droite; c'est également la tangente de l'angle que fait la droite avec l'horizontale (l'axe des x). Et, c'est en PLUS … la dérivée en M de la courbe étudiée.	La pente est égale à l'accroissement en y par rapport à l'accroissement en x. 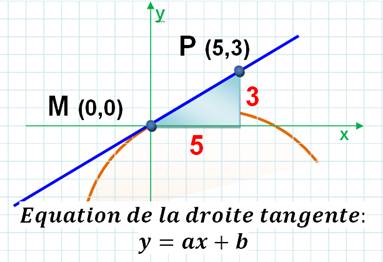La tangente est une droite et son équation générique est ax + b. Nous connaissons deux points de la droite (M et P) qui nous permettent de préciser les valeurs de a et b.

Bilan

Pente, tangente, coefficient directeur, dérivée sont des mots qui ont à voir avec la même notion. Celle d'un accroissement en y pour un accroissement donné en x. C'est un taux de variation.

La vitesse est aussi un taux de variation de la distance parcourue selon le temps. La vitesse est effectivement la dérivée de la distance par rapport au temps

Dérivée
La dérivée est une généralisation de la notion de tangente à une courbe. Par exemple pour une parabole (courbe en x²) c'est une fonction qui donne le coefficient directeur de la tangente en tous les points de la courbe; tout le long de la courbe. Dans cet exemple où y = f(x) = 2x² – 8, le graphe de la fonction est une parabole (rouge). Vous apprendrez que la dérivée de f(x) est y' = f'(x) = 4x. 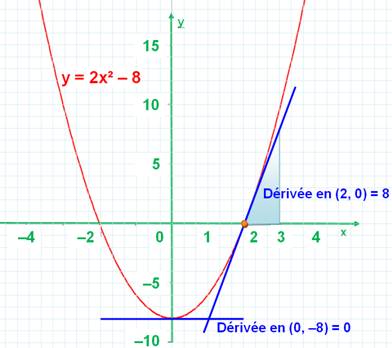Ce qui veut dire que pour:	Au point bas de la parabole (0, –8), la dérivée est nulle, la tangente est horizontale. Au point (2, 0), la dérivée vaut 8 et pour une progression de 1 en x, la progression en y est bien 8.

Précisions sur les notations

La dérivée de la fonction f(x) est notée f'(x).

La dérivée de sa représentation graphique y est notée y'.

Pour le curieux:

Si l'on veut préciser que la dérivée se fait par rapport:

à x, on note:

à la fois x et y, on note:

au temps, on note: .

Le "d", comme delta, rappelle que l'on manipule des quantités infiniment petites.

Dérivée et intégrales
La dérivée caractérise une vitesse de variation. En classe de première, vous allez apprendre à calculer la dérivée des principales fonctions. Il existe un calcul inverse: connaissant les vitesses de variations tout le long de la courbe, trouvez la courbe! C'est le calcul des intégrales. >>> Note: la dérivée se généralise à des polynômes de degré quelconque. La dérivée d'un polynôme de degré k aura un degré k – 1.	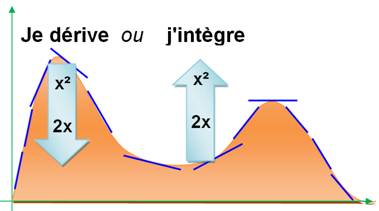En dérivant, le degré du polynôme décroît. Par exemple: d'une courbe délimitant une surface, je passe à des droites qui "enveloppent" la courbe. En intégrant, le degré du polynôme augmente. Par exemple: de droites enveloppant une surface, je passe à la courbe. Pour mémoriser: en dérivant je passe des "m²" au "m" et inversement en intégrant.

Exemple de calcul d'une dérivée
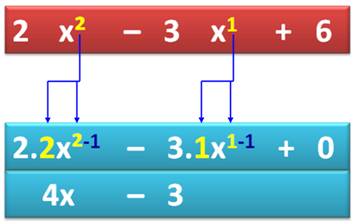
La technique opératoire pour les polynômes est simple: le degré du monôme devient coefficient multiplicateur, chaque monôme est baissé d'un degré, et une constante donne une dérivée nulle. Ainsi: f(x) = 2x² – 3x + 6 a pour dérivée: f'(x) = 4x – 3.
Exemple montrant la technique opératoire selon les degrés des monômes (en bleu la dérivée): Attention: le 1 de la dérivée vient du x de la fonction et non du 1 qui, lui, donne une dérivée nulle. Autre exemple, impliquant les racines (Rappel: puissance ½ est équivalent à racine carrée; ainsi x^2/3 veut dire racine cubique du carré de x):

Voir Initiation via les carrés et les cubes des nombres / Liste de dérivées usuelles

Suite	Exemples résolus Dérivées Intégrale – Approche avec 1/x Primitive
Voir	Dérivées – Glossaire Équations différentielles – Glossaire Infinitésimaux Physique en seconde Vitesse - Glossaire
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Analyse/AnaDerSe.htm