|
|||||||||||||||||||||||||||||||||
![]()
|
ÉQUATIONS du DEUXIÈME DEGRÉ Initiation Exemple simple de résolution
conduisant à la notion de dérivée
sur une fonction du deuxième degré. |
|
|
|
|
|
|
|
Le
chiffre
d'affaires est le montant d'argent qu'il recevra pour sa vente (c'est le
montant des factures qu'il va
engranger). Stock de 1 700 kg à 1,20 euros / kg => 1 700 x
1,20 = 2 040 euros |
|
|
|
|
Récolte
quotidienne: 75 kg / jour
Prix
des pommes de terre
Tous les jours le prix
diminue de 3 centimes par kg
Le
prix au kg me semble bien faible; je me conforte en refaisant le calcul: 3 x
30 = 90 centimes de baisse sur les 30 jours. Oui, c'est beaucoup. Espérons
que ce n'est pas un cas réel! Chiffre
d'affaires: (1 700 + 2 250) x 0,3 = 1 185 euros |
|
|
|
La
question précédente nous a préparés à cette formulation algébrique.
|
|
|
|
Pour
le calcul du chiffre d'affaires, ne pas oublier la récolte initiale. R(n) = (1700 + Q(n) ) x P(n) = (1700 + 75 n) x (1,20 –
0,03n) = 1700 x 1,20 – 1700 x 0,03 n +
75 x 1,20 n – 75 x 0,03 n² = – 2,25 n² + 39 n + 2 040 |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
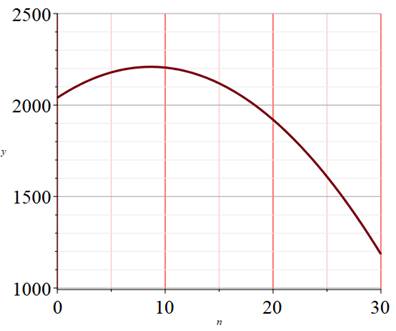
Graphe
pour disposer de l'allure de la fonction. Je constate que la courbe passe par
un maximum vers n = 9.
Tableau des valeurs
pour les 30 jours
Je vérifie que
j'obtiens bien les valeurs calculées précédemment pour n = 0 et n = 30. |
|
|
|
Le
maximum est atteint au neuvième jour pour
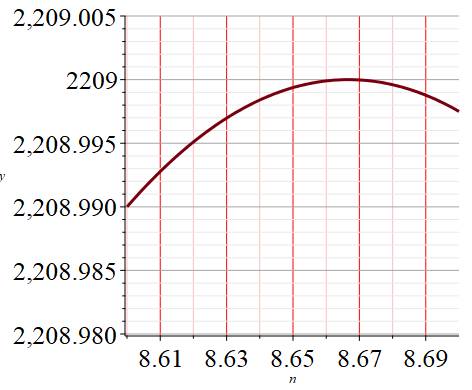
un chiffre d'affaires de 2 208,75 euros. Pour information:
valeur exacte pour le jour 8,666… et pour 2 209 euros. Un
graphe détaillé montre ces valeurs:
|
|
|
|
|
Cet
exercice constitue une introduction à l'étude des polynômes
du second degré ax² + bx
+ c. Ceux-ci
sont très importants en physique. Par exemple, la courbe de l'exercice
pourrait être la trajectoire
d'un projectile (avec le temps en abscisse). Le point haut est le moment
ou le projectile atteint son maximum avant de retomber. Deux
types de questions vont alors se poser avec les polynômes: -
quels sont les points de passages
par des extremums, et -
quels sont les points de passages
par l'ordonnée 0. L'étude des extremums
conduira à la notion de dérivée. Une nouvelle
notion qui va suivre l'élève de seconde durant toutes ses études à partir de
maintenant. Pas de panique: dérivée veut dire simplement tangent à la courbe ou encore vitesse de variation ou encore pente. On
peut retenir: En physique, on parle de vitesse; en
maths, on dit dérivée. La courbe de détail
ci-dessus montre que le maximum est atteint pour n = 8,666… et y = 2 209. Le
calcul de la dérivée permet de trouver ces valeurs exactes sans faire le
tableau ni la courbe. Pour info voici le calcul:
R(n) = – 2,25 n² + 39 n + 2 040 On calcule la dérivée*
: 2 . (-2,25) n + 39 = - 4.5 n + 39 Et cette dérivée est
égale à 0 pour 8,666… * On verra plus tard
dans le cours comment on fait. C'est
Newton et
Leibniz (indépendamment et en s'en disputant la paternité) qui ont mis au
point ces méthodes de calcul à la fin des années 1600. Depuis,
on sait calculer la trajectoire des
planètes et bien d'autres choses. Voir Dérivée
en première – Technique de calcul L'étude du passage par 0,
ou point d'intersection de la courbe avec l'axe des x, va conduire à la
résolution des équations
du second degré. Par exemple: x² – 3x +
2 = 0 pour x = 1 et x = 2. Ces deux valeurs
s'appellent les racines de l'équation. Dans le cas de R(n) de
l'exercice, si le fermier s'acharnait à produire des pommes de terre, son
chiffre d'affaires serait nul au 40e jour (jour où le kg vaut 0
euro) La courbe passe
également par 0 pour n = -22,666… À raison de 75 kg par jour, le fermier
aurait commencé sa récolte il y a 22,666 … jours pour obtenir les 1 700 kg qu'il a aujourd'hui. (22,666 x 75 = 1 700). |
|
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()