|
||||||||||||||||||||||||||||||||||||||||
![]()
|
MULTIPLICATION FACTORISATION Les multiplications seules, c'est sans
problème. Avec les additions, méfiance! |
Voir Toutes les
notations possibles de la multiplication
|
Quelle
est la valeur du produit algébrique suivant: (x
– a) (x – b) (x – c) … (x – z) = ? |
Voir Lettres
de l'alphabet / Identités
remarquables
Bon à savoir
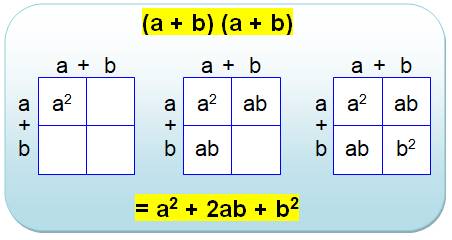
|
|
||
|
|
a b |
|
|
Les objets se multiplient en les plaçant
l'un à côté de l'autre (s'il y a confusion, on place un point). Voir
Symboles de la multiplication |
a
x b = ab = a.b |
|
|
|
3
a 2
b |
|
|
Chaque objet amène son coefficient
et ils se multiplient entre eux. |
3
x 2 ab = 6 ab |
|
|
|
3
a 2
a |
|
|
Le même objet multiplié par lui-même donne un
carré. On note avec un exposant "carré" ou "puissance 2". |
6
aa = 6 a² |
|
|
|
3
a² 2
a |
|
|
On note en exposant (petit chiffre en haut à
droite) la quantité de a multipliée entre eux. |
6
aaa = 6 a3 |
|
|
|
3
a 2
abc |
|
|
Les objets se combinent selon les règles
données ci-dessus. |
6
a²bc |
|
|
|
3
a3b2c 2
a2b2c3 |
|
|
Les objets se combinent selon les règles
données ci-dessus: Les
coefficients se multiplient. Les exposants
s'ajoutent. |
6
a5b4c4 |
|
|
|
||
|
|
a b
+ c |
|
|
a multiplie chaque objet de la
parenthèse. |
a
(b + c) = ab + ac |
|
|
|
3a b
+ c |
|
|
Le coefficient 3 s'applique à chaque objet. |
3a
(b + c) = 3ab + 3ac |
|
|
|
3a 2b
+ 5c |
|
|
Les coefficients se multiplient. |
3a
(2b + 5c) = 6ab + 15ac |
|
|
|
3ax 2by
+ 5cxyz |
|
|
Même si l'objet est complexe, les lettres
se combinent. |
3ax (2by + 5cxyz) =
6abxy + 15acx²yz |
|
|
Analogie avec l'écriture
factorisée |
|
|
|
|

Voir Triangle
Voir Génotypes et leurs développements
|
|
||
|
|
ab
+ ac |
|
|
Parmi les deux termes présentés, a
est un facteur commun. Rappel du vocabulaire ab et ac sont les deux termes
de la somme a et b sont les deux facteurs
du produit ab. Remarquez que vous
savez déjà faire l'opération dans l'autre sens; celle-ci n'est pas plus
difficile. |
ab
+ ac = a (b +
c) |
|
|
|
a
+ ac |
|
|
Se souvenir que le coefficient 1 devant a est sous-entendu. |
a
+ ac = 1a + ac
= a (1 + c) |
|
|
|
6ab
+ 4ac |
|
|
Les coefficients se factorisent aussi. Il
s'agit de trouver le plus grand commun diviseur (PGCD)
des coefficients. |
6ab + 4ac = 2x3 ab + 2x2 ac = 2a (3b + 2c) |
|
|
|
acx² + adxz + bcxy + bdyz |
|
|
Pas facile! On remarque a et x en commun dans
les deux premier termes. Et by
dans les 2 derniers. |
acx² + adxz + bcxy + bdyz =
ax (cx + dz) + by (cx + dz) |
|
|
Surprise! Le même facteur entre
parenthèses. On le nomme F. |
= ax F + by F = ( ax + by ) F = ( ax + by ) ( cx + dz ) |
|
|
|
|||
|
Factoriser |
F = |
(b – 1) x b + (b – 1) x 1 |
|
|
Résultat |
F = |
(b – 1) (b + 1) |
|
|
Question classique du
débutant: Pourquoi dans les
deux premières parenthèses on a des "–" et dans les deuxièmes parenthèses un "–" et un "+" ? |
|||
|
1) Réponse directe |
F = |
(b – 1) x b + (b – 1) x 1 |
|
|
Addition de deux termes |
|
(b – 1) x b &
(b – 1) x 1 |
|
|
Élément commun |
|
(b – 1)
x b
&
(b – 1) x 1 |
|
|
Mise en facteur de cet élément commun |
|
(b – 1)
x (b
+ 1) |
|
|
Résultat |
F = |
(b – 1) (b + 1) |
|
|
2) Réponse imagée |
F = |
(b – 1) x b + (b – 1) x 1 |
|
|
Pour ne pas être impressionné (gêné), je baptise l'élément commun |
|
b – 1 = C |
|
|
|
F = |
C
x b + C x 1 |
|
|
Imaginons que C soit des bonbons |
F = |
J'ai b
bonbons et 1 de plus |
|
|
Je dispose en tout de |
F = |
(b + 1) bonbons |
|
|
Refaisons le chemin à l'envers |
F = |
(b + 1) C |
|
|
|
F = |
(b + 1) (b –
1) |
|
|
3) Autre chemin |
F = |
(b – 1) x b
+ (b – 1) x 1 |
|
|
Développons cette expression |
|
b
x b – b x 1 + 1 x b – 1 x 1 |
|
|
|
|
b² –
b + b
– 1 |
|
|
|
F = |
b² – 1 |
|
|
(a² – b² = (a – b) (a + b) |
F = |
(b – 1) (b + 1) |
|
|
Quelle
est la valeur du produit algébrique suivant: (x
– a)(x – b)(x-c) … (x – z) = ? (x
– a)(x – b)(x-c) … (x – x) … (x – z) = 0 |
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()
