Pavage, une approche

Pavage – Approche
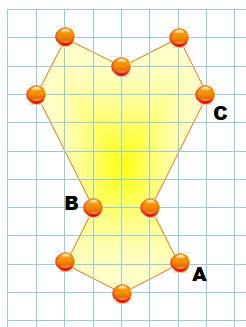
Problème On se propose d'étudier la forme indiquée. plus précisément, la capacité de cette forme à paver le plan. Pavage, c'est quoi? Mot emprunté aux carreleurs qui signifie qu'il est possible de recouvrir le sol d'un carrelage fait avec des carreaux de cette forme. Autrement-dit: cette forme peut être reproduite et les copies assemblées jointivement pour recouvrir la surface (en maths, on dit le plan; pensez au plan de travail). Encore une image: avec cette forme on peut réaliser les pièces d'un puzzle. Oui, mais il faudrait faire quelque chose pour s'arrêter aux bords. En fait, sans cela, on parle d'un pavage infini.
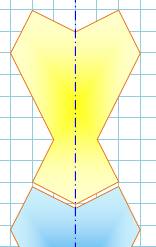
Mes premières observations Cette forme est constituée d'une ligne brisée fermée, un polygone à dix côtés avec des parties saillantes (convexes) et des parties en creux (concaves). Elle est symétrique: en la coupant en deux par une ligne verticale, je peux disposer de deux morceaux identiques par retournement (ou, image l'un de l'autre dans un miroir). Je note également que le haut est concave et le bas convexe, et l'un peut s'emboiter dans l'autre. Pour effectuer un pavage cela peut être utile.

Question n°1

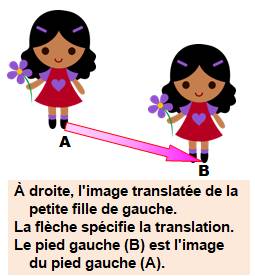
Construire l'image de ce polygone par translation qui transforme B en C.

Interprétation

Translation est un mot de maths qui signifie, en gros, glissement.

Effectuer une translation, c'est tout simplement faire glisser la figure telle quelle, sans la déformer, ni surtout la faire tourner.

Bon! Maintenant, il faut savoir de combien la faire glisser. En général, on donne un segment avec une flèche qui indique la direction, le sens et la distance de glissement.

Note: comme toujours en maths, il faut des noms! Cette flèche s'appelle un vecteur. Un objet d'études pour le lycée et d'une très grande importance en physique (pour représenter une force).

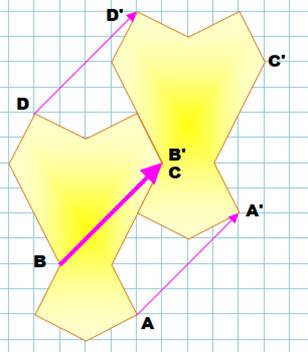
Dans notre cas, que devient le polygone en le faisant glisser de façon que le point B passe en C

On dessine la flèche de translation qui part de B et qui s'arrête en C.

On fait glisser toute la figure de cette quantité. On note tous les points images en mettant une apostrophe: A', B', C' et D'. On lit: A prime, B prime, etc.

Le point B', image de B par la translation, est bien passé en position C.

Notez que la flèche de translation s'applique à tous les points de la figure (évidemment!).

Je note bien que les deux figures s'emboitent. Bon gage pour effectuer un pavage.

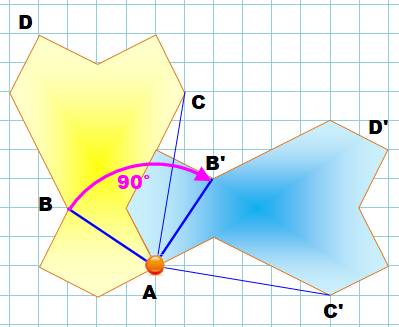
Question n°2

Construire l'image du polygone initial par la rotation de centra A et d'angle 90° dans le sens des aiguilles d'une montre.

Rotation

Pour une fois, ce mot se comprend facilement.

Pour effectuer la rotation on dessine un trait partant du centre de rotation A (le pivot; là où je placerais la pointe du compas). Je choisis un point quelconque de la figure comme extrémité. Disons B.

Je trace un cercle et m'arrête à 90° dans le sens des aiguilles de la montre. L'image B' de B est là.

Je peux faire la même chose avec C pour me rassurer.

Je fais pivoter toute la figure de sorte que A reste en A et B prend la place B'.

En faisant pivoter la figure d'un quart de tour autour de A, je trouve une figure qui s'emboite dans la figure originelle. Deuxième bon gage pour effectuer un pavage.

Question n°3

Poursuivre la construction pour obtenir le pavage du plan représenté par cette feuille à carreaux.

Pavage

Nous avons observé une possibilité de pavage avec chacune des transformations étudiées (la translation et la rotation)

Combinons les deux et nous avons ce magnifique pavage (ou carrelage ou puzzle, comme vous voudrez).

Une autre idée de pavage simple avec cette forme

Jouez avec ces pavages

Voir Pavages d'Escher, le maitre!

Bilan (à retenir)

Nous avons appris ce qu'est le pavage du plan.

Nous savons également construire deux transformations importantes dans le plan: la translation et la rotation.

La translation est définie par une flèche qui est appelée vecteur.

La copie d'un objet après transformation est appelée son image.

Retour	Pavage – Débutants (cas des triangles)
Suite	Pavage avec hexagones Transformations
Voir	Carrés parfaits Construction géométrique des nombres Dodécagone Géométrie – Index Hexagone – Généralités Méandres Pavage mystérieux du triangle Pentominos Poincaré Carré Dominos Golygone à huit côtés Hexagone – pavage Pavage d'Ammann-Beenker Pavage de Penrose Polygone Théorème de la carpette (ou du tapis) Triangle équilatéral
Cette page	http://diconombre.fr/Pavage/Approche.htm