NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 31/03/2023 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Outils mathématiques
Débutants Général	GROUPES			Glossaire Ensemble
INDEX Structures algébriques Accueil Sommaire	Introduction	Triangles et carrés	Groupe – Définition
	Types de groupes	Groupe cyclique	Groupes de permutations
		Nombres et groupes	Groupe des symétries
		Sommaire de cette page >>> Le quart de tour >>> Multiplication >>> Dans la cour >>> Solidarité >>> Retour sur le quart de tour >>> Retour sur la multiplication

Au lieu de points, de droites et de plans, on pourrait tout aussi bien employer les mots tables, chaises et vidrecomes (verres à bière).

David Hilbert – Congrès des mathématiques de Paris en 1900

Voir Pensées & humour / Autres citations

GROUPES – Introduction

avec des exemples

Dans le monde des ensembles, le groupe est une entité qui a révolutionné les mathématiques. Il possède des propriétés communes à tous les objets de la même famille. Une fois définies, inutiles de passer son temps à les redécouvrir. Efficacité …

Analogie informatique: en programmation, une fois un objet défini en donnant ses propriétés, ses attributs, on l'utilise autant que l'on veut sans avoir à le redéfinir à chaque usage. On se facilite grandement la vie …

LE QUART DE TOUR
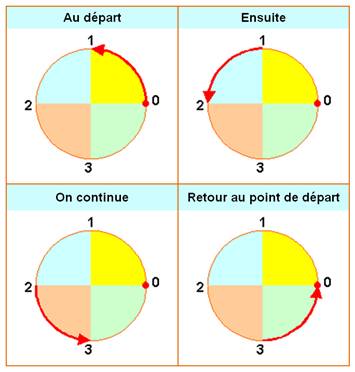
On tourne en rond On imagine un jeu avec un cercle. Avec une certaine LOI de mouvement: je me déplace dans un seul sens. Et, à chaque fois, d'un quart de tour. Et alors ? Au bout de quatre mouvements, je me retrouve au point de départ. Pas très malin tout ça ! Oui mais, faisons un tableau qui donne les points d'arrivée selon le point de départ et la quantité de mouvements (quarts de tour) exécutés. Ouais !!! Une table d'addition ? Ça ressemble: 0 + 0 = 0 0 + 1 = 1 1 + 2 = 3 etc. Pas tout à fait: 3 + 1 = 0 et non pas 4 3 + 2 = 1 et non pas 5 En fait, chaque fois que l'on dépasse 4, on soustrait 4. Avec ce petit artifice, le tableau est particulièrement sympathique.	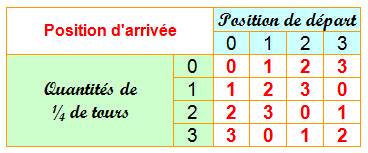Mouvements successifs Tableau des positions d'arrivée Le tableau de composition des quarts de tour est symétrique. Ce tableau, qui ressemble à nos tables d'additions ou de multiplications, est appelé: table de Cayley (1854).

Voir Congruence pour une table d'addition semblable / Morphisme / Arthur Cayley

MULTIPLICATION
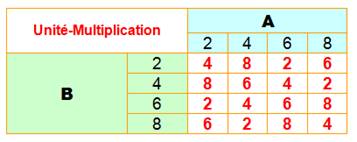
Rapprochons nous des nombres On imagine un autre jeu pour l'exemple. Le terrain de jeu comprend les nombres pairs 2, 4, 6 et 8. La LOI sur ce terrain est la multiplication de deux de ces nombres A et B dont on ne conserve que les unités du produit. Quelle chance ! Les résultats sont toujours: 2, 4, 6 ou 8. Les mêmes valeurs que celles du départ. On reste dans son petit monde.	Table de multiplication L'opération sur les nombres spécifiés crée un monde clos.

DANS MA COUR … ou pas!
Un monde clos. Est-ce si banal ? Est-ce vrai pour toutes les OPÉRATIONS ? Toutes les LOIS? Voici des exemples.
Dans le désert	Nombres
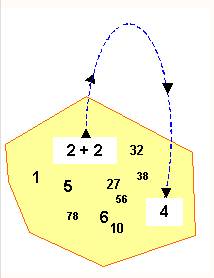
Je suis dans le désert et je lance un caillou en l'air. Il retombe toujours sur le sable.	Avec les nombres entiers, je fais une addition. Le résultat est un entier: 2 + 2 = 4
Dans le désert	Nombres
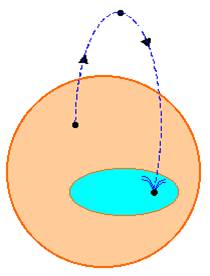
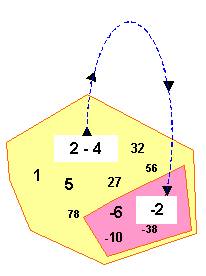
Je suis dans le désert avec un lac (ou oasis) et je lance un caillou en l'air. Il retombe sur le sable ou dans l'eau.	Avec les nombres entiers, positifs et négatifs, je fais une soustraction. Le résultat est un entier positif ou négatif. 2 – 4 = – 2
Bilan Les deux cas existent: opérations dans un monde clos, et opérations qui débordent sur un monde voisin. Les premières sont intéressantes, car, quoiqu'on fasse, on reste entre-nous. On est toujours sûr que le résultat sera un individu de la famille. Comme dans l'exemple de la multiplication, vu ci-dessus.

Voir Constructions des ensembles de nombres

SOLIDARITÉ
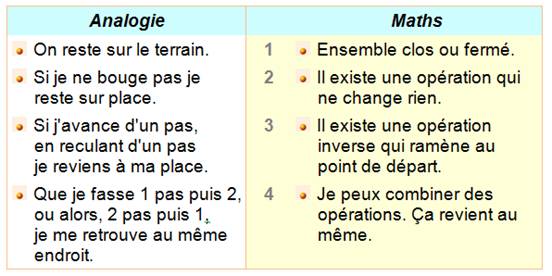
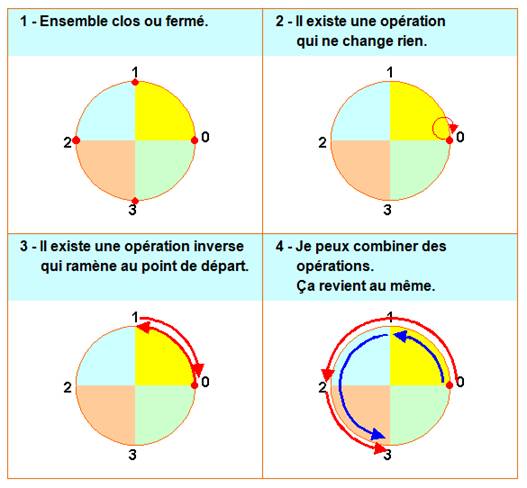
Pour jouer, il faut TROIS CONDITIONS
Et un peu d'harmonie EN QUATRE POINTS
Cette sorte de solidarité forme un GROUPE	On a baptisé tous les objets (les ensembles) ayant ces propriétés du nom de GROUPE. La définition plus mathématique est donnée au chapitre suivant.

LE QUART DE TOUR, un groupe?
TROIS CONDITIONS
et QUATRE POINTS
D'une manière générale La rotation d'un point M de centre O et d'angle quelconque forme un GROUPE.

La MULTIPLICATION, un groupe?
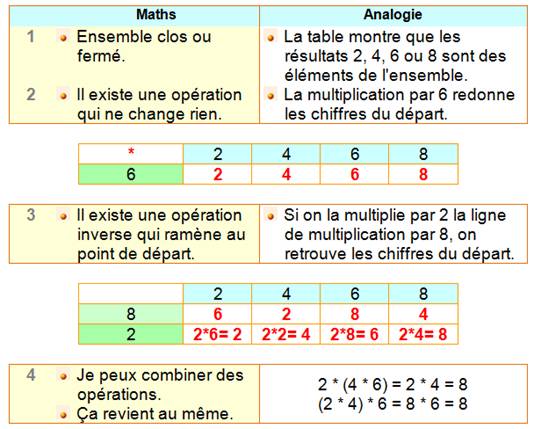
TROIS CONDITIONS
et QUATRE POINTS
D'une manière générale La multiplication des nombres entiers forme un GROUPE

Retour	Théorie des nombres – Introduction
Suite	Groupe – Définition Débutants – Index Structures algébriques – Index Outils mathématiques – Index Classes de congruence Classes de congruence avec diviseurs de n
Voir	Calcul – Index Ensemble – Glossaire Les symétries Les types de nombres Logique – Index Théorie des nombres – Index
Cette page	http://villemin.gerard.free.fr/Referenc/Outils/AOUTILS/GrouIntr.htm