NOMBRES – Curiosités, Théorie et Usages

Accueil DicoNombre Rubriques Nouveautés Édition du: 23/05/2022

Orientation générale  DicoMot Math Atlas Actualités M'écrire

Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths

RUBRIQUE ENSEMBLES

Débutants

Général

Groupe de Lie E₈

Glossaire

Général

Le E8 est un exemple d'un groupe de Lie, concept découvert en 1887 par le mathématicien Norvégien Sophus Lie pour étudier la symétrie.

Sommaire de cette page >>> Mars 2007 >>> E8 – C'est quoi? >>> Applications >>> Calculs >>> Historique

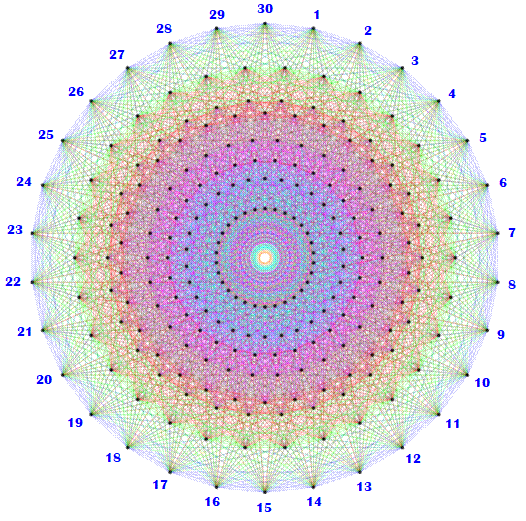
Anglais: the object known as the exceptional Lie group E₈

Représentation du groupe de Lie E

Mars 2007 – Une équipe internationale reconstitue un puzzle mathématique à 248 dimensions
Le 19 mars 2007, l'Institut Américain de Mathématiques annone le décodage du E8. Il a fallu quatre ans à une équipe de 18 mathématiciens et informaticiens américains et européens pour obtenir ce résultat.	The American Institute of Mathematics (AIM), one of the leading math institutes in the U.S., announced today that after four years of intensive collaboration, 18 top mathematicians and computer scientists from the U.S. and Europe have successfully mapped E8, one of the largest and most complicated structures in mathematics.

E8 – En gros, c'est quoi?
La sphère, le cylindre ou même le cône sont des objets en trois dimensions dont on peut étudier les propriétés de symétries: E8 représente les symétries d'un objet à 57 dimensions; E8 lui-même possède 248 dimensions. E8 est l'une des structures mathématiques les plus complexes, qui avait été découverte au XIX^e siècle. E8 est un exemple d'un groupe de Lie. C'est l'une des trois formes réelles de ce groupe complexe. Les groupes de Lie se trouvent au croisement de deux domaines mathématiques fondamentaux: l'algèbre et la géométrie.	Si les groupes sont des vallées Il existe parmi eux des groupes compliqués qui seraient les montagnes. Le groupe E8, très compliqué, serait un haut sommet. Les mathématiciens ont inventé les groupes de Lie afin de capturer l'essence de la symétrie: la découverte de tout objet symétrique, tel qu'une sphère, est un groupe de Lie.

APPLICATIONS
Faciliter les calculs par ordinateur permettant de résoudre des problèmes complexes. Essentiel pour saisir des phénomènes dans de nombreuses disciplines mathématiques et de la science dont l'algèbre, la géométrie, la théorie des nombres, la gravité quantique, la chimie.	Les physiciens rencontrent E8 régulièrement lorsqu'ils tentent d'unir la gravité à d'autres forces fondamentales dans une théorie consistante de gravité quantique. Le décodage du E8 pourrait les aider à établir une théorie unifiée.

CALCULS
Les calculs de l'E8 sont en fait une analyse de la symétrie. description de chacun des blocs qui composent l'E8 Et relations entre eux. Calcul sur une matrice à 205 263 363 600 entrées avec 453 060 lignes et autant de colonnes. Utilisation d'un supercalculateur 77 heures de calcul 60 giga-octects de mémoire 16 processeurs.	Séquençage du génome humain > 1 gigaoctet Décodage et représentation du E8 60 gigaoctets (45 jours de musique en MP3) Nom de code du projet: The Atlas of Lie Groups and Representations

HISTORIQUE

1889 – Découverte de E8 par Sophus Lie, un mathématicien norvégien (1842-1899). 1894 – Elie Cartan étudie le groupe de Lie E8. 1960 – Peter McMullen en dessine à la main une représentation à 2 dimensions. John Stembridge reprend ce dessin par ordinateur (polytope nommé 421). (en médaillon dans le titre de cette page). John H. Conway a montré la relation entre ce polytope et E8. 2007 – Le 19 mars, l'Institut Américain de Mathématiques annone le décodage du E8.

Suite	Groupe Théorie des ensembles – Index Structures algébriques – Index
DicoNombre	Nombre 30
Sites	Mathematicians Map E8 Visualizing the E8 root system
Cette page	http://villemin.gerard.free.fr/aMaths/Ensemble/E8.htm