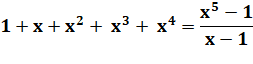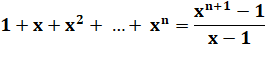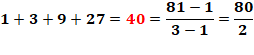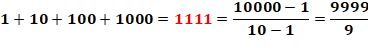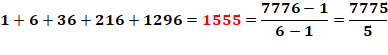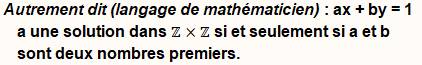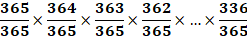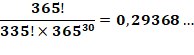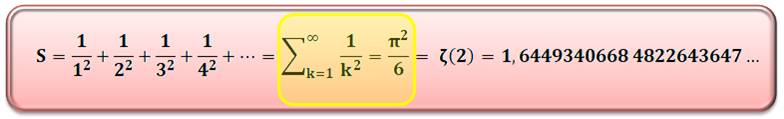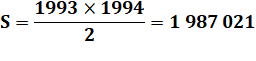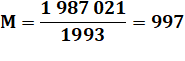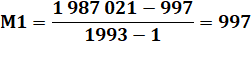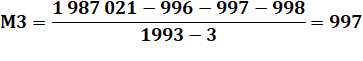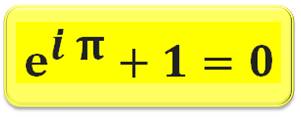NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 18/05/2025 Orientation générale DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Maths en se divertissant
Débutants Général	BRÈVES de MATHS									Glossaire Général
INDEX Brèves Atlas des maths	Page 1	Page 10		Page 20		Page 30		Page 40			Page 50

	Index général		Page 1 (1-19)		Page 2 (20-39)		Page 3 (40-59)		Page 4 (60-79)
	Page 5 (80-99)		Page 6 (100-119)		Page 7 (120-139)		Page 8 (140-159)		Page 9 (160-179)

BRÈVES de MATHS – Page 9

Un millier de faits et chiffres

sur les nombres et les mathématiques

Ces pages sont dédiées à tous ceux qui veulent aborder les mathématiques en douceur et en s'amusant tout en découvrant les aspects les plus fondamentaux de cette discipline. Un parcours à picorer avec nombreux liens d'orientation vers les développements destinés à satisfaire votre curiosité.

En principe ces pages sont très abordables sans connaissances particulières de maths. Elles sont proposées dans un ordre quelconque favorisant la découverte de sujets multiples.

Anglais: Facts and figures about numbers and mathematics

160. Identité en 1 + x + x² + …
Cas particulier
Cas général
Quelques cas particuliers
Liste des nombres en puissance Sauriez-vous retrouver la valeur de n et de x pour chacun?		7, 13, 15, 21, 31, 40, 43, 57, 63, 73, 85, 91, 111, 121, 127, 156, 255, 259, 341, 364, 400, 511, 585, 781, 820, 1023, 1093, 1111, 1365, 1555, 2801, 3280, 3906, 4681, 5461, 7381, 9331, 9841, 11111, 19531, 19608, 21845, 29524, 37449, 55987, 66430, 87381, 97656, 111111, 137257, 299593, 335923, 349525, 488281, 597871, 960800, 1111111, 2015539, 2396745, 2441406, 5380840, 6725601, 11111111, 12093235, 19173961, 47079208, 48427561, 111111111, 153391689, 435848050, 1111111111 …
Pour en savoir plus	>>> Identités remarquables >>> Identités spéciales		>>> Nombre 40 >>> Nombre 1 111 >>> Nombre 1 555

161. Théorème de Bézout
Théorème Deux entiers naturels a et b sont premiers entre eux si et seulement s’il existe deux entiers relatifs x et y tels que : ax + by = 1 Note : Z est l’ensemble des entiers relatifs ; deux fois Z est une convention pour signifier qu’il y deux nombres à trouver.			Étienne Bézout (1730-1783) a laissé son nom à un théorème connu avant lui de Gaspard Bachet de Mérizac (1650). Il l’a généralisé en l’appliquant à la divisibilité des polynômes. On appelle aussi cette propriété par théorème de Bachet-Bézout
Exemple a = 25 = 5 x 5 et b = 18 = 2 x 3² Ces deux nombres sont premiers entre eux. L’équation de Bézout est: 25x + 8y = 1 Pour trouver ces nombres, on utilise l’algorithme d’Euclide (tableau).		Résultat : –5a + 7b = 1 à comparer à ax + by = 1 a = –5 et b = 7 Selon le théorème de Bézout 25 et 18 sont donc premiers entre eux.
Prolongeons la recherche : quelles sont toutes les solutions de l’équation initiale ?
Brèves liées	>>> Algorithme d'Euclide – B 104 >>> Théorème de la divisibilité – B181
Pour en savoir plus	>>> Premiers entre eux >>> Théorème de Bézout			>>> Ensemble des entiers relatifs >>> Algorithme d’Euclide

162. Galilée (Galileo Galilei) – 1564-1642 (78 ans)
Biographie Mathématicien, physicien, astronome et écrivain. Il avait commencé par des études de médecine. Né à Pise (Toscane – Italie) en 1564. Décès à Arcetri (quartier proche de Florence) en 1642. Trois enfants avec sa compagne, Marina Gamba. De physicien, il deviendra astronome et fera de nombreuses découvertes avec sa lunette. Physicien Il commence à formaliser les lois physiques en utilisant les mathématiques. Il étudie notamment la chute des corps et détermine que: la durée de la chute est indépendante de la masse ou encore que la période du pendule est liée à sa longueur. Il est célèbre, lui aussi, pour avoir établi la loi de la relativité du mouvement. Astronome Il découvre la lunette hollandaise en 1609, alors considérée comme un jouet. Il l'améliore: d'un grossissement 3, il passe à 30. Il observe le ciel et découvre le relief de la Lune, les étoiles de la Voie lactée et surtout les satellites de Jupiter (1610). Les taches solaires montrent que le Soleil n'est pas parfait, ce qui déplait à l'Église. Héliocentrisme de Copernic Galilée a toujours été convaincu, surtout après l'observation des satellites de Jupiter, que la Terre tourne autour du Soleil. L'héliocentrisme est une théorie prônée par Copernic, qui s'oppose au géocentrisme. En 1623, Urbain VIII devient pape. Ami de Galilée, il l'autorise à parler de l'héliocentrisme.		Dialogue entre les deux plus grands systèmes du monde Galilée imagine un dialogue entre, Simplicius, un défenseur des anciennes croyances et Sagredo qui soutient les idées de Salviati. Ce livre indispose l'Inquisition. Galilée est convoqué devant le tribunal en 1633. Il décide d'abjurer afin de sauver sa vie. Il est assigné à résidence. Occasion d'écrire un nouveau livre en 1638: Discours concernant deux sciences nouvelles. Galilée est réhabilité par l'Église en 1992. Galilée à son procès Tableau de J. Nicolas (Musée du Louvre) - Extrait Et pourtant elle tourne (E pur si muove) Phrase légendaire attribuée à Galilée à l'issue de son procès en 1633. Elle est apocryphe: il n'y a aucune preuve que Galilée ait tenu ces propos. Il est probable que cette phrase lui ait été attribuée lorsqu'il était encore en vie.
Brèves associées	>>> Newton
Pour en savoir plus	>>> Galilée – Biographie >>> Galilée – Relativité / Principe d'inertie >>> Copernic		>>> Chute des corps >>> Pendule >>> Jupiter

163. Nombre 9 – NEUF

Amusement

Nombres parlants ou plus correctement allographes. Lisez: c'est un vin neuf.

Propriétés

Le nombre 9 est impair. C'est le carré de 3:
9 = 3 x 3 = 3²

C'est la somme des cubes des deux premiers nombres: 9 = 1³ + 2³.

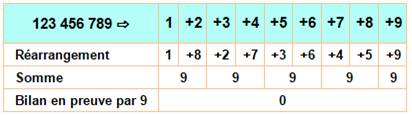
Le nombre 9 est aussi la somme des factorielles des trois premiers nombres: 9 = 1! + 2 ! + 3 ! = 1 + 2 + 6.

Divisibilité par 9

La somme des chiffres d'un nombre (réduite au maximum) indique le reste de sa division par 9.

Ex: 28 / 9 = 3 x 9 + 1 et 2 + 8 = 10 puis 1 + 0 = 1

Donc, si la somme des chiffres est divisible par 9, le nombre l'est aussi.

123 456 789 est divisible par 9 (= 9 x 13 717 421),

comme tous les nombre comprenant ces neuf chiffres.

Un nombre diminué de la somme de ses chiffres est divisible par 9.

Ex: 28 – (2 + 8) = 18 = 2 x 9

Un nombre diminué de son retourné (le plus grand moins le plus petit) est divisible par 9.

Ex: 987 – 789 = 198 = 9 x 22

Table de multiplication du 9

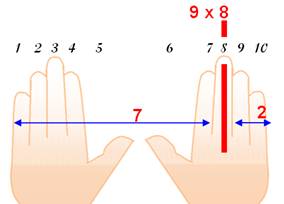
Les dizaines vont en croissant et les unités en décroissant, créant cette belle symétrie.

Table du 9 avec les doigts

Pour 8 x 9, il y a 7 doigts avant le 8 et 2 après: on donne immédiatement: 8 x 9 = 72. Essayez avec d'autres nombres.

Curiosités numériques

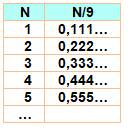
Un nombre de 1 à 8 divisé par 9 produit un nombre décimal avec ce nombre répété à l'infini.

Brèves associées

>>> Nombre 8

>>> Factorielle

>>> Nombre 10

Pour en savoir plus

>>> Nombre 9 – Culture

>>> Nombre 9 – Maths

>>> Allographes

>>> Multiplication par 9

>>> Divisibilité par 9

>>> Preuve par 9

164. Premiers en quantité infinie
Le premier qui la prouvé C'est Euclide, vers 300 av. J.-C., qui démontre qu'il existe une quantité infinie de nombres premiers. Sa démonstration est originale. Son astuce: créer le nombre: N = 2x3x5x7x11 ….x P + 1 Ajouter 1 au produit de tous les nombres premiers en supposant qu'ils sont en quantité finie, le plus grand étant P. Exemples 2x3x5x7 + 1 = 211, un nombre premier. 2x3x5x7x11x13 + 1 = 30 031 = 59 x 509, un nombre composé. Le plus grand nombre premier connu, découvert en janvier 2018, comporte plus de 20 millions de chiffres et s'exprime avec une puissance de 2 2^{77 239 917}– 1 Anglais (notez la tournure de phrase) Euclid's theorem asserts that there are infinitely many prime numbers.		Démonstration d'Euclide Il suppose qu'il n'a que k nombres premiers, pas un de plus. Son raisonnement l'amène à trouver un nouveau nombre premier. Ce qui contredit son hypothèse. C'est que les nombres premiers sont en quantité infinie. Le nombre d'Euclide Euclide prend les k nombres premiers et les multiplie. Le produit est évidemment divisible par chacun des nombres premiers. L'astuce est de lui ajouter un. Alors la division par chacun des nombres premiers est impossible: Il reste toujours 1. La contradiction Le nombre d'Euclide est un nouveau nombre. Il est plus grand que tous les nombres premiers. De deux chose l'une: ou c'est un nouveau nombre premier, ce qui contredit l'hypothèse; ou c'est un nombre composé: le produit d'au moins deux nombres premiers. Or, il n'est pas divisible par l'un des premiers du lot initial. C'est qu'il existe d'autres premiers. Bilan Dans les deux cas possibles, la conclusion conduit à admettre l'existence d'un nouveau nombre premier. Et, le raisonnement peut être reconduit en incluant ce nouveau nombre premier. Conclusion: il y en a une infinité.
Brèves associées	>>> Nombres premiers >>> Premiers en 6k+1 et 6k+5		>>> Infini
Pour en savoir plus	>>> Infinité de nombres premiers >>> Le plus grand nombre premier connu		>>> Euclide >>> Anglais à savoir

165. Anniversaire – Paradoxe
Incroyable! Parmi 30 personnes, quelle est la probabilité de trouver deux personnes ayant le même anniversaire: 70 %. En demandant d'estimer cette probabilité, la valeur donnée dépasse rarement 10%. Personne n'imagine que cette probabilité est aussi élevée. Test en classe Ainsi, avec une classe de 30 élèves, il est presque certain de tomber sur deux individus ayant le même anniversaire. Par contre, le jour en question est une surprise. Il suffit de 23 personnes pour atteindre 50% de probabilité.		Calcul pour 30 personnes La probabilité que A soit né un jour de l'année est 365/365. La probabilité que B ne soit pas né le même jour que A est 364/365. Pour C, il doit être né encore un autre jour. La probabilité est 363/365. Etc. La conjonction de ces événements: En arrangeant cela: C'est la probabilité qu'aucun des 30 n'ait le même anniversaire. La probabilité que deux aient le même anniversaire est!
Brèves associées	>>> Jeu de dés
Pour en savoir plus	>>> Anniversaire le même jour (explications détaillées)		>>> Dénombrement >>> Probabilités

166. Al-Khwârizmî (vers780-850)
Biographie Né à Khwarezm ou Huwarizm (aujourd'hui Khiva) en Ouzbékistan, il a vécu à Bagdad à la cour du calife Al-Maamoun. Muhammad ibn Musa al-Khawarizmi est un mathématicien, géographe, astronome et astrologue perse. Il est aussi connu sous son nom latin Algoritmi. Ses écrits, rédigés en langue arabe et traduits en latin favorisent le développement de l'algèbre en Europe. Traité d'algèbre Kitāb al-mukhtaṣar fī ḥisāb al-jabr wa-l-muqābala (l'Abrégé du calcul par l'opposition et la restauration).		Algorithme Du fait de sa méthode de calcul, son nom est resté pour désigner une procédure de calcul, puis de traitement informatique. Un algorithme est une étape primordiale avant toute programmation. Algèbre Le mot al-jabr figure dans le titre de son traité. Il veut dire accomplissement, restauration, réunion. Allusion à une opération importante servant à résoudre les équations: addition d'une même quantité de chaque côté de l'égalité. Nombres / Chiffres arabes Al-Khwarizmi est l'un des principaux vecteurs de diffusion du système de numération indien, connu désormais avec les chiffres dits "arabes" ou "indo-arabes".
Brèves associées	>>> Équation		>>> Thalès >>> Pythagore
Pour en savoir plus	>>> Al-Khawarizmi >>> Chiffres arabes		>>> Algorithme >>> Numération décimale >>> Numération – Historique

167. Somme des inverses des carrés
La somme des inverses des carrés des nombres successifs est convergente et vaut Pi au carré divisé par six. Ce nombre est appelé zêta de deux et il est égal à 1,644…
Nombreux sont les mathématiciens qui ont essayé de calculer cette somme. C'est Euler en 1735 qui a donné la solution. Depuis, ce calcul, dit problème de Bâle (lieu de naissance d'Euler), fait l'objet de nombreuses questions en licence de maths.		Le calcul arithmétique de cette série est laborieux. Si vous arrivez à calculer mille termes sans erreur, vous n'aurez que les deux premiers chiffres après la virgule. Voilà qui explique les recherches infructueuses des mathématiciens avant Euler. La somme Pi² / 6 se décompose en somme des inverses au carré pour: Pi² / 24 les nombres pairs, et Pi² / 8 les nombres impairs.
Brèves associées	>>> Somme des inverses des nombre
Pour en savoir plus	>>> Somme des inverses des carrés >>> Constante Pi		>>> Euler (1707-1783) >>> Nombre 1,644…

168. Poules et œufs – Énigme
Voir Brève 62-1236
Brèves associées	>>> Œufs au marché	>>> Chapeaux – Énigme >>> Lapins et canards
Pour en savoir plus	>>> Énigmes classiques >>> Moyenne	>>> Jeux et énigmes – Index

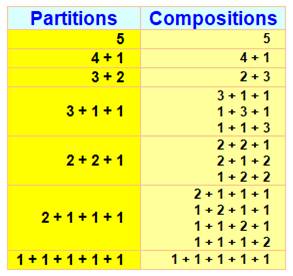
169. Partitions des nombres entiers
Addition ou multiplication Un nombre entier est toujours soit un nombre premier soit le produit unique de nombres premiers (10 = 2 x 5). C'est une propriété multiplicative (fondamentale) des nombres entiers. Et avec l'addition ? Dans ce cas, chaque nombre entier peut être décomposé en somme d'entiers: le nombre 5 peut être décomposé de 14 façons différentes; et de 7 façons différentes, si on ignore l'ordre des termes. Partitions et compositions Les termes de ces additions s'appellent des parts d'où le nom de partition. On trouve aussi le terme plus savant de sommants. En tenant compte de l'ordre des sommants, on obtient les décompositions (ou compositions) d'un nombre entier. Recherches Quelles sont les quantités de partitions ? Comment trouver toutes les partitions ? Identification de partitions particulière comme un carré somme de deux carrés (triplets de Pythagore).			Partitions et compositions du nombre 5 Quantité pour le nombre entier 5: Partitions: 7 " à deux sommants: 2 Compositions: 14 " avec les nombres 1 et 2: 8
Brèves associées	>>> Théorie des nombres	>>> Triplets de Pythagore
Pour en savoir plus	>>> Partitions – Introduction	>>> Théorème fondamental de l'arithmétique

170. Archimède – Sphère et cylindre
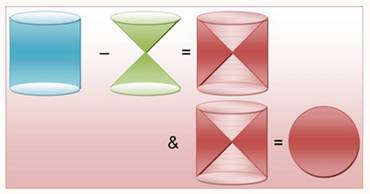
Archimède et sa découverte Archimède est fier de sa découverte. Il a démontré que le volume de la sphère est égal au deux tiers de celui du cylindre. Il a procédé par exhaustion: approximation par des volumes qui encadre le volume cherché. En l'occurrence: 2/3 V_C < V_S < 2/3 V_C sont deux inégalités impossibles. Selon sa volonté, sa tombe porte une sphère inscrite dans un cylindre. Les trois volumes Aujourd'hui on calcule les volumes avec les formules connues. Le volume de l'espace non occupé par la sphère inscrite dans le cylindre est exactement égal à celle du sablier (deux cônes tête-bêche). Proportions V_Sablier = 1, V_Sphère = 2, V_Cylindre = 3		Équations en volume 3 – 1 = 2 (cylindre évidé) et 2 = 2 Calcul des volumes
Brèves associées	>>> Démonstration en géométrie
Pour en savoir plus	>>> Cylindre, sablier et sphère >>> Archimède (–287 à – 212)		>>> Sphère >>> Cylindre

171. Procédé de Kaprekar
Procédé itératif Il consiste à ordonner les chiffres d'un nombre par ordre décroissant (Max) et également par ordre croissant (Min) et à effectuer leur soustraction (D = Max – Min). La différence (D) est soumise à nouveau à ce même procédé. Exemple: 14 => 41 – 14 = 27 => 72 – 27 = 45 … Nombres à deux chiffres Le cycle de Kaprekar de tous les nombres à deux chiffres se termine par 0. Exemple: 13, 18, 63, 27, 45, 9, 0. Nombres à trois chiffres et plus Le cycle de Kaprekar des nombres à trois chiffres se termine par 495, et par 0 pour quelques uns. Exemple: 102, 198, 792, 693, 594, 495. Avec quatre chiffres, c'est 6 174 ou 0. Exemple: 1 004, 4 086, 8 172, 7 443, 3 996, 6 264, 4 176, 6 174. Avec cinq chiffres, il y a apparition de boucles.		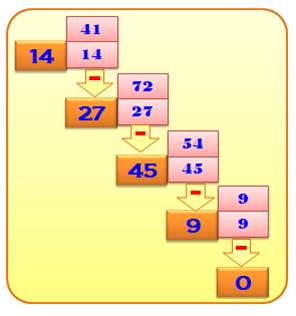Kaprekar pour le nombre 14 Propriété Dès le premier calcul les nombres trouvés sont des multiples de 9.
Brèves associées	>>> Magie de la preuve par 9		>>> Divisibilité
Pour en savoir plus	>>> Procédé de Kaprekar >>> Divisibilité par 9		>>> Nombre 495 >>> Nombre 6 174

172. Cinq nombres divisibles par 3
Parmi cinq nombres quelconques, pas nécessairement distincts, il en existe toujours trois dont la somme est divisible par 3 (S3). Parmi quatre nombres, la probabilité d'obtenir S3 divisible par 3 est: 70,3%. Et pour trois nombres, elle est de 34,4%.		Sachant que le reste de la division par 3 est 0, 1 ou 2, on déduit: Cas 1 Si trois restes parmi les cinq sont égaux, leur somme est divisible par 3. Exemple avec le reste 2: 2 + 5 + 11 = 18, divisible par 3. Cas 2 Dans le cas contraire, les seuls combinaisons de restes possibles sont: (0, 0, 1, 1, 2) ou (0, 0, 1, 2, 2) ou (0, 1, 1, 2, 2), sinon, il y en aurait trois égaux. En choisissant les nombres dont les restes sont (0, 1, 2), la somme sera divisible par 3. Exemple: 3 + 4 + 5 = 12, divisible par 3.
Brèves associées	>>> Diviseurs d'un nombre		>>> Critères de divisibilité
Pour en savoir plus	>>> Cinq nombres et somme divisible par 3

173. Factorielle 9
Factorielle n Produit des nombres de 1 à n. Noté n! avec un point d'exclamation. Ainsi: 3! = 1 x 2 x 3 = 6 Factorielle 9 Comment trouver les facteurs de ce nombre ? Le facteur 2 se trouve: une fois dans 2, deux fois dans 4, une fois dans 6 et trois fois dans 8, soit sept fois au total. Donc: 9! est divisible par 2⁷ = 128. Le facteur 3 s'y trouve quatre fois. Donc: 9! est divisible par 3⁴ = 81. Il est aussi divisible par 5 et par 7, donc par 35. On peut d'ailleurs écrire: 9! = 128 x 81 x 35. Quantité de diviseurs Prenez les exposants de la factorisation (7, 4, 1, 1); ajoutez un à chacun (8, 5, 2, 2); faites le produit: 8x5x2x2 = 160 diviseurs.		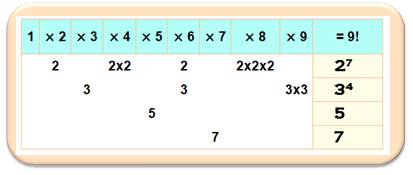Factorisation de factorielle 9 Diviseurs de factorielle 9 Ce nombre (9!) possède 160 diviseurs, dont jusqu'à 100: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 24, 27, 28, 30, 32, 35, 36, 40, 42, 45, 48, 54, 56, 60, 63, 64, 70, 72, 80, 81, 84, 90, 96. Famille amusante de diviseurs: 18, 108, 1 008, 1 080, 10 080.
Brèves associées	>>> Factorielle et le loto		>>> Division >>> Critères de divisibilité
Pour en savoir plus	>>> Factorielles >>> Factorielle 9 >>> Facteurs et diviseurs		>>> Quantité de diviseurs >>> Nombre 18

174. Entier manquant
Énigme Parmi les nombres de 1 à 1993, on retire trois entiers consécutifs, et la moyenne est un nombre entier. Quels sont ces trois nombres ? Raisonnement Comme pour l'astuce de la somme des entiers, on peut aussi constituer des paires symétriques: 1 + 1193 = 2 + 1192 = … Retirer certaines de ces paires ne change pas la moyenne. Retirer le nombre central non plus. Solution Il faut simplement retirer l'élément central et ses deux voisins: 996, 997, 998.		Calculs Somme des entiers de 1 à 1993 Moyenne Sans le nombre central: 997 Sans ses deux voisins
Brèves associées	>>> Somme des entiers		>>> Nombre et ses chiffres >>> Divisibilité par 45 de aaaabbbb
Pour en savoir plus	>>> Énigmes de l'entier manquant >>> Somme des entiers de 1 à n		>>> Jeux et énigmes – Index

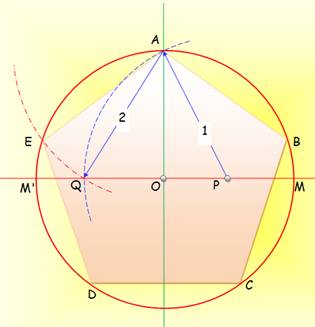
175. Pentagone – Construction
On dispose (on sait construire) d'un cercle et de deux diamètres perpendiculaires qui positionne le point A, l'un des sommets du pentagone, et du milieu P du rayon OM. Deux étapes simples pour trouver le sommet E: 1) cercle PA => point Q, et 2) cercle AQ => point E Note Côté du pentagone: AQ Côté du décagone: OQ Il suffit d'écarter le compas de la longueur OQ et de reporter cet écart sur le cercle pour construire le décagone.
Brèves associées	>>> Pentagone Meccano	>>> Hexagone >>> Octogone
Pour en savoir plus	>>> Pentagone – Construction >>> Pentagone >>> Décagone	>>> Constructions élémentaires >>> Polygones – Index >>> Nombre 5

176. Horloge mathématique
Sur cette horloge, les nombres ont été remplacés par des expressions mathématiques. Sauriez-vous les reconnaitre ? Les commerçants proposent de nombreux types de telles horloges. Un recensement des indications portées sur le cadran se trouve sur la page indiquée en "en savoir plus". Note: il existe quelques erreurs dues à la recopie du dessin du cadran. Par exemple à 3 heures, il faut lire Pi et non 11.
Brèves associées	>>> Dix en chiffres	>>> Énigme du parking
Pour en savoir plus	>>> Horloges mathématiques >>> Horloges – Fonctionnement	>>> Constante Pi

177. Nombre 153 & la pêche
Pêche miraculeuse L'Évangile selon Saint Jean relate la pêche miraculeuse dans le lac de Tibériade par sept disciples de Jésus, dont Saint Pierre: 153 poissons. La question: que signifie 153 ? Peut-être la quantité des espèces de poissons connues à cette époque ou alors un rapport avec les nombreuses propriétés mathématiques du nombre 153. Cubes et 153 La somme itérée des chiffres au cube de tout multiple de 3 finit par 153. Suite en Brève 210 Calendrier et 153 153 = 2 x 30 + 3 x 31 C'est la somme des jours sur cinq mois pleins ne comprenant par le mois de février.		Propriétés arithmétiques 153 = 3² x 17 (facteurs). 153 = 17 x (1 + 5 + 3) = 3 x 51 (chiffres de 153). 153 = 1001 1001₂ = 99₁₆ (palindromes). 153 = 1 + 2 + 3 + 4 + 5 + 6+ 7 + 8 + 9 + 10 + 11 + 12 + 13 + 14+ 15 + 16 + 17 – Nombre triangulaire. 153 = 1³ + 5³ + 3³ (somme des cubes des chiffres). 153 = 1! + 2! + 3! + 4! + 5! (Somme des cinq premières factorielles).
Brèves associées	>>> Nombre 153 et cycle-cube >>> Nombre 153 et cubes		>>> Nombre 100
Pour en savoir plus	>>> Nombre 153 et ses propriétés >>> La pêche miraculeuse >>> Cycle-cube en 153		>>> Nombres triangulaires >>> Palindromes >>> Factorielles >>> Quantite de jours en k mois

178. La plus belle formule
Beauté Une propriété majeure des mathématiques d'une grande beauté. Mais comment les mathématiciens qualifient-ils la beauté ? Dans le cas de cette formule, les mathématiciens y voient une relation intime entre domaines qui semblent totalement indépendants: Géométrie avec Pi; Algèbre des nombres réels avec e; Algèbre des nombres complexes avec i; et Nombres entiers de base avec 0 et 1, éléments neutres de l'addition et de la multiplication.		La plus belle formule Relation d'Euler Vision numérique de la relation Sachant que le i² = -1
Brèves associées	>>> Identités remarquables		>>> Nombres complexes
Pour en savoir plus	>>> Relation d'Euler		>>> Euler – Biographie

179. Fraction et série infinie
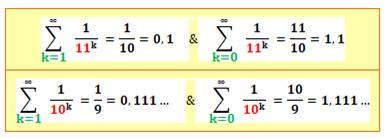
Comment faire 1 avec des 11 ? Incroyable! En ajoutant les fractions suivantes en 1/11, fractions qui sont de plus en plus petites, on obtient le nombre 0,1. Multiplions le tout par 10 pour obtenir 1. 1/11 + 1/11² + 1/11³ … = 0,09090…+ 0,00826… + 0,00075… + … = 0,0999… = 0,1 Avec k = 1 et jusqu'à k = 24, la somme comporte k fois le chiffre 9 en tête des décimales. Pour k = 24, la somme vaut: 0,99999999999999999999999989847… Il y en a encore plus ensuite.		Séries avec 1/11 et 1/10 Lecture de la première formule: la somme, depuis k égal un et jusqu'à k tendant vers l'infini, de la fraction un sur onze à la puissance k est égale à un dixième, soit zéro virgule un.
Autre exemple (formule en bas à gauche) En prenant les fractions 1/10, la somme devient 0,111 … qui correspond à la fraction 1/9.		Généralisation En choisissant des fractions en 1/n, on obtient pour somme la fraction 1/(n – 1).
Brèves associées	>>> Somme des inverses des nombres		>>> 0,999… = 1
Pour en savoir plus	>>> Nombres périodiques et séries infinies		>>> Fractions

Retour	Brèves de maths – Page 8
Suite	Brèves de maths – Page 10
Voir	Voir liens en haut de page
Cette page	http://villemin.gerard.free.fr/NombDico/aBreves/Breve09.htm

160. Identité en 1 + x + x² + …

161. Théorème de Bézout

162. Galilée

(Galileo Galilei) – 1564-1642 (78 ans)

163. Nombre 9 – NEUF

164. Premiers en quantité infinie

165. Anniversaire – Paradoxe

166. Al-Khwârizmî (vers780-850)

167. Somme des inverses des carrés

168. Poules et œufs – Énigme

169. Partitions des nombres entiers

170. Archimède – Sphère et cylindre

171. Procédé de Kaprekar

172. Cinq nombres divisibles par 3

173. Factorielle 9

174. Entier manquant

175. Pentagone – Construction

176. Horloge mathématique

177. Nombre 153 & la pêche

178. La plus belle formule

179. Fraction et série infinie