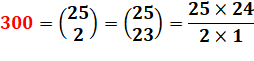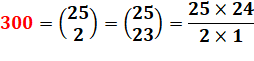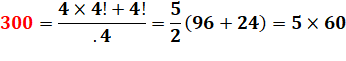nombre 300

3 + 0 + 0 = 3	· Somme des chiffres égale au produit des chiffres non nuls.
300 / (2 + 3 + 5) = 30 300 / (2 + 3 + 5)² = 3		· Divisible par la somme des chiffres de ses facteurs et même par le carré de la somme.
CCC ou XV^XX ou III^C 100+100+100 ou 15 x 20 ou 3 x 100			· Formes romaines et médiévales.
300 base 7 → 606 300 base 8 → 454 300 base 9 → 363			· Palindrome selon trois bases successives

Addition et soustraction

300 = 1 + 2 + … + 24

· Une des cinq sommes de nombres consécutifs >>>

· Nombre triangulaire T₂₄.

300 = 149 + 151

300 = 13 + 14 + … + 47

· Somme de deux premiers consécutifs (jumeaux).

· Somme de dix nombres premiers consécutifs.

Multiplication et division

300 = 15 x 20 = 12 x 25

· Quinze fois vingt.

Remarquez la similitude des chiffres:
300 = 15 x 20 = 12 x 25.

293, 300, 307

· Interpremier.

Avec les puissances

300 = 2² + 10² + 14²

= 10² + 10² + 10²

= 5² + 5² + 5² + 15²

= 2² + 4² + 6² + 10² + 12²

· Sommes de carrés >>>

300 = 10² + 10² + 10²

· Somme de trois carrés identiques >>>

En puissances

300

· Le produit de trois cents (ou moins) entiers de la forme 6n + 1 n'est jamais une puissance parfaite – R. Oblath, 1942 (cité par Le Lionnais)

Jeux et combinatoire

		· Coefficient du binôme ou nombre de Pascal. Quantité de combinaisons de 2 ou 23 parmi 25
300 = 1 + 2 + 3 + 45 x 6 + 7 + 8 + 9 = 1 – 23 x 4 + 56 x 7 + 8 – 9 = – 1 – 23 x 4 + 56 x 7 – 8 + 9 = – 1 x (2 + 3) x 4 + 56 x 7 – 8 x 9 = 1 + 234 + 56 + (–7 + 8) x 9			· Opérations pannumériques.
			· Jeu du quatre 4. Avec la notation .4 = 0,4 = 2/5 · Solution avec deux 4. Avec notation .4 surligné qui vaut 0,444… = 4/9
300	· Quantité de segments à l'intersection des faces d'un dodécaèdre régulier. Cent-quatre-vingts sont bornés.

Culture

Quantité	· 300 fois chacun des chiffres de 1 à 9 dans les nombres de 0 à 999. Seulement 190 fois le "0".	>>>
Calendrier	· 27 octobre: le 300^e jour d'une année normale.	>>>
Jeux	· 300 points: score maximum au bowling.	>>>
Histoire	· TRECENTO : le XIV^e siècle italien. Renaissance (mot italien, de tre, trois, et cento, cent)	>>>
Physique	· 300 lumens par watt: espoir de rendement lumineux pour les diodes électroluminescentes.	>>>
Biologie	· 300 kg / hectare densité des lombrics dans nos sols	>>>
Construction	· 300, 65 m Hauteur de la Tour Eiffel à sa construction en 1889.	>>>
Transport	· Airbus A300	>>>

Identité détaillée

n = 300

En français : trois cents

En anglais (US) : three hundred

------------------------------------------------------------

Somme des chiffres : 3

Type harshad : Oui

Produit des chiffres : 0

------------------------------------------------------------

Premier inférieur = 293

Premier supérieur = 307

------------------------------------------------------------

Factorisation : 2^2 × 3 × 5^2

Liste des facteurs : {2, 3, 5}

Quantité de facteurs : 3

Somme distincts : 10

Somme multiplicité : 10

Produit distincts : 30

------------------------------------------------------------

Diviseurs : [1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 25, 30, 50, 60, 75, 100, 150, 300]

Quantité : 18

Somme des diviseurs : 868

Somme stricte : 568

Type : Abondant

Semi-parfait : Oui

Moyenne des diviseurs : 48.22

Somme des carrés : 136710

------------------------------------------------------------

Indicatrice d'Euler φ(n) : 80

Fonction de Möbius μ(n) : 0

Sommes d'entiers consécutifs = n :

[300]

[99, 100, 101]

[58, 59, 60, 61, 62]

[34, 35, …, 41]

[13, 14, …, 27]

[1, 2, …, 24]

Quantité = 5

------------------------------------------------------------

Sommes de premiers consécutifs = n :

[13, 17, 19, 23, 29, 31, 37, 41, 43, 47]

[149, 151]

Quantité = 2

------------------------------------------------------------

Somme de premiers distincts (<4) :

[2, 5, 293]

[2, 17, 281]

[2, 29, 269]

[2, 41, 257]

[2, 47, 251]

[2, 59, 239]

[2, 71, 227]

[2, 101, 197]

[2, 107, 191]

[2, 131, 167]

[7, 293]

[17, 283]

[19, 281]

[23, 277]

[29, 271]

[31, 269]

[37, 263]

[43, 257]

[59, 241]

[61, 239]

[67, 233]

[71, 229]

[73, 227]

[89, 211]

[101, 199]

[103, 197]

[107, 193]

[109, 191]

[127, 173]

[137, 163]

[149, 151]

Quantité = 31

------------------------------------------------------------

Sommes de k carrés :

3 fois : 2² + 10² + 14² = 300

3 fois : 10² + 10² + 10² = 300

4 fois : 1² + 1² + 3² + 17² = 300

4 fois : 1² + 3² + 11² + 13² = 300

4 fois : 1² + 5² + 7² + 15² = 300

4 fois : 1² + 7² + 9² + 13² = 300

4 fois : 2² + 2² + 6² + 16² = 300

4 fois : 2² + 6² + 8² + 14² = 300

4 fois : 3² + 7² + 11² + 11² = 300

4 fois : 5² + 5² + 5² + 15² = 300

4 fois : 5² + 5² + 9² + 13² = 300

4 fois : 6² + 8² + 10² + 10² = 300

4 fois : 7² + 7² + 9² + 11² = 300

Quantité = 13

Voir Diviseurs, Quantité, Somme, Fonctions arithmétiques

Numération

Particularités

=== Conversion de 300 ===

------------------------------

2 | 100101100

3 | 102010

4 | 10230

5 | 2200

6 | 1220

7 | 606

8 | 454

9 | 363

10 | 300

11 | 253

12 | 210

13 | 1, 10, 1

14 | 176

15 | 150

16 | 12, 12

17 | 10, 11

18 | 16, 12

19 | 15, 15

20 | 15, 0

21 | 14, 6

22 | 13, 14

23 | 13, 1

24 | 12, 12

25 | 12, 0

26 | 11, 14

27 | 11, 3

28 | 10, 20

29 | 10, 10

30 | 10, 0

31 | 9, 21

32 | 9, 12

60 | 50

=== Repdigits ===

base 19 → 15, 15

base 24 → 12, 12

base 29 → 10, 10

base 49 → 66

base 59 → 55

base 74 → 44

base 99 → 33

base 149 → 22

base 299 → 11

=== Pannumérique ===

base 3 → 102010

base 4 → 10230

=== Consécutif croissant ===

base 22 → 13, 14

base 298 → 12

=== Consécutif décroissant ===

base 12 → 210

base 42 → 76

base 300 → 10

=== Palindromes ===

base 7 → 606

base 8 → 454

base 9 → 363

base 13 → 1, 10, 1

base 19 → 15, 15

base 24 → 12, 12

base 29 → 10, 10

base 49 → 66

base 59 → 55

base 74 → 44

base 99 → 33

base 149 → 22

base 299 → 11

Voir Bases / Brésiliens

Retour

Suite

· Nombres en 290

· Nombres en 310

Voir

· Nom des nombres

· Nombres géométriques

Voir

· Nombres par leur nom

· Empreinte des nombres

· DicoNombre Junior

· Historique de ce site et Références

· Maitres en nombres

Cette page

http://villemin.gerard.free.fr/NombDico/N100a500/Nomb300/Nb300.htm