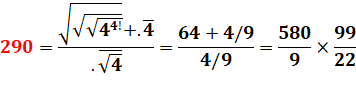Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 28/12/2021 M'écrire Brèves de Maths

Débutant Glossaire Types de nombres Nom des nombres Écriture des nombres Table des facteurs Langues	Dictionnaire des Nombres
	0 / 0,… / 1 / 10 / 50 / 100		200 à 300		300 / 400 / 500 / 600 / 700 / 800 / 900 / 1 000 / 2 000 / 5 000 / 10 000 / 100 000 / 10^6 / 10^9 / 10^100
	200	210	220	230	240	250	260	270	280	290
	290	291	292	293	294	295	296	297	298	299

Faites un double-clic pour un retour en haut de page

Deux-cent-quatre-vingt-dix

Deux-cent-nonante

Two hundred ninety

Nouvelle orthographe

avec des traits d'union partout

Facteurs
Binaire	1 0010 0010
Bases	20212 10117 AA28
Romain	CCXC

Suite en propriétés arithmétiques

Composé

Cunningham

Déficient

Glissant

Intouchable

Mian-Chowla

Non-totient

Pair

Simple

Sphénique

Ternaire équilibré (101202)

Chiffres et numération

290 – (2 x 9) = 272	Devient palindrome lui retirant le produit de ses chiffres non nuls.
290 – 1 = 17² 290/2 – 1 = 12²	Nombre et sa moitié produisant des carrés.

Addition et soustraction

290 = 5 + 6 + … + 24	Une des trois sommes de nombres consécutifs >>>
290 = 67 + 71 + 73 + 79	Somme de premiers successifs.
290 = T10 + T11 + T12 + T13 = 2n² + 8n + 10 avec n = 10	Somme de nombres triangulaires consécutifs.

Multiplication et division

	Nombre glissant.
	Somme des carrés des diviseurs. Somme des cubes des diviseurs (rare !).

Avec les puissances

290 = 1² + 17² = 11² + 13² = 8² + 8² + 9² + 9²	Sommes de carrés. Deux seules sommes de carrés >>>
290 = 1^3 + 1^3 + 2^3 + 4^3 + 6^3 = 1^4 + 1^4 + 2^4 + 2^4 + 4^4	Sommes de puissances.

Jeux

Jeu du quatre 4. Avec la notation anglaise: .4 = 0,4 = 2/5; .4 surligné = 0,444… = 4/9 et . racine de 4 surligné = 0,2222 … = 22/99

Culture

Théorie des nombres

Théorème des 290 sur les formes quadratiques représentant les entiers.

>>>

Identité détaillée

Voir Diviseurs, Quantité, Somme, Fonctions arithmétiques

Numération: base, [chiffres]			Repdigit (Brésilien)
2, [1, 0, 0, 1, 0, 0, 0, 1, 0] 3, [1, 0, 1, 2, 0, 2] 4, [1, 0, 2, 0, 2] 5, [2, 1, 3, 0] 6, [1, 2, 0, 2] 7, [5, 6, 3] 8, [4, 4, 2] 9, [3, 5, 2] 10, [2, 9, 0] 11, [2, 4, 4]	12, [2, 0, 2] 13, [1, 9, 4] 14, [1, 6, 10] 15, [1, 4, 5] 16, [1, 2, 2] 17, [1, 0, 1] 18, [16, 2] 19, [15, 5] 20, [14, 10] 21, [13, 17]	22, [13, 4] 23, [12, 14] 24, [12, 2] 25, [11, 15] 26, [11, 4] 27, [10, 20] 28, [10, 10] 29, [10, 0] 30, [9, 20] 60, [4, 50]	28, [10, 10] 57, [5, 5] 144, [2, 2] 289, [1, 1]

Voir Bases / Brésiliens

Retour Suite	Nombre 289 Nombre 291
Voir	Nom des nombres Nombres géométriques
Voir	Nombres par leur nom Empreinte des nombres DicoNombre Junior Historique de ce site et Références Maitres en nombres

Cette page

http://villemin.gerard.free.fr/NombDico/N100a500/Nomb200/Nb290.htm