|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
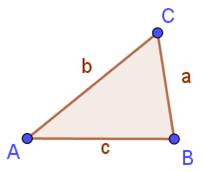
DIAGONALES Quantité de triangles dans les polygones Trouver le nombre
de triangles dans une figure simple n'est pas compliqué avec un peu de
méthode. Souvent l'objet de devinettes de concours. Ici, nous allons découvrir
les triangles formés par les diagonales dans un polygone dans le cas le plus général (polygones
non-réguliers). Quantités de triangles dans un polygone
… 11 297, 17 234, 25 935, 37 424, 53 516, 73 404, 101 745, 136 200, 181
279, 236 258, 306 383, 389 264, 495 650, 620 048, 772 785, 951 384, 1 167
453, 1 410 350, 1 716 191, 2 058 848, 2 463 384, 2 924 000, 3 462 305, 4 067
028, 4 776 219, 5 568 786, 6 479 551 … |
Voir Noms
des polygones
Triangles
formés par les diagonales
|
Déterminer la quantité
de triangles formés en joignant les sommets d'un polygone est très simple:
c'est la quantité
de combinaisons de trois points parmi n sommets:
Nous cherchons plus:
tous les triangles visibles formés par toutes les intersections. Le décompte
est plus complexe. |
Pour l'hexagone Q = 20
et les triangles formés sont: [A, B, C], [A, B, D], [A, B, E], [A, B, F], [A, C, D], [A, C, E], [A, C, F], [A, D, E], [A, D, F], [A, E, F], [B, C, D], [B, C, E], [B, C, F], [B, D, E], [B, D, F], [B, E, F], [C, D, E], [C, D, F], [C, E, F],
[D, E, F] |
|
|
|||
|
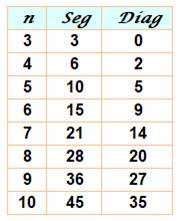
S'il est
évident qu'il n'y a qu'un seul triangle
dans un triangle, profitons-en pour faire le point sur la quantité de segments
dans les polygones. Note: Quantité de
diagonales = quantité
de segments moins quantité de
côtés. |
|||
|
Triangle
|
Segments
|
|
|
|
|
||
|
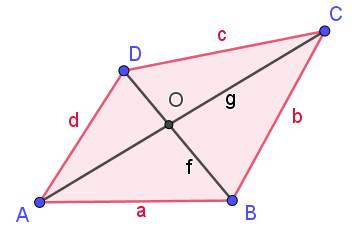
Tous les triangles Combien
de triangles visibles dans ce quadrilatère
? Pas très compliqué: 4 petits et 4 plus gros; total 8. Voyons selon
la méthode exhaustive:
|
Les HUIT triangles du quadrilatère
|
|
|
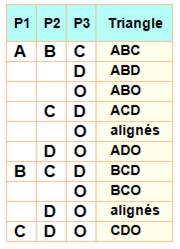
Combien de triangles pour relier
quatre points ? Combien
faut-il de triangles, au minimum, pour relier tous les sommets d'un
quadrilatère ? La
réponse est trois. Pourquoi ? Chaque
triangle relie trois points, soit deux couples de points. Le problème
consiste donc à dessiner des triangles tels que tous les couples de points
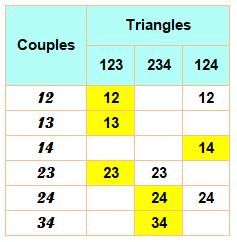
soient reliés avec le minimum de redondances. Une solution La colonne de gauche montre les six couples de
points à relier. En plaçant les triangles 123 et 234, par exemple,
seuls cinq couples sont couverts, nécessitant un triangle de plus, par
exemple 124.
|
Trois triangles sont nécessaires pour couvrir
tous les sommets du quadrilatère
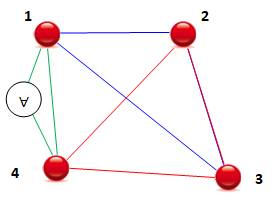
Après avoir choisi les triangles 123 et 234, il existe deux possibilités
pour atteindre le couple 14:
Notation: le A renversé veut
dire: quelconque, ou au choix. Ici, les traits verts peuvent être réunis au
point 2 ou au point 3, au choix. La généralisation à tout polygone n'est pas
évidente. |
|
|
||||
|
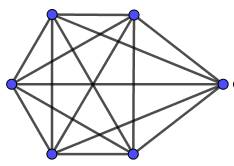
Méthode Un
décompte soigné montre que cette figure, formée avec un pentagone
quelconque et ses diagonales, comporte 35 triangles. Mais, comment
en être absolument sûr ? En
utilisant une sorte de table de multiplication dont le résultat est 1 si les
deux points sont reliés et 0 sinon. Ce
tableau est appelé matrice,
mais inutile de connaitre les propriétés des matrices pour aborder notre
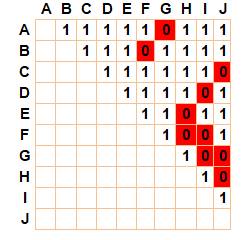
problème. Lecture de la matrice Sur la première ligne, le point A est relié aux
points: B, C, D, E, F, H, I et J; alors que le point G ne l'est pas. Sur la deuxième ligne, le point B est relié aux
points: C, D, E, G, H, I et J; alors que le point F ne l'est pas. Etc. Commentaires Inutile de mentionner le point A avec le point A. De même, on ne note que les connexions avec les
points suivants dans l'ordre alphabétique pour ne pas répéter les connexions
déjà notées. Remarques Dans un pentagone, il y a un maximum de trois
triangles sans superposition. La figure comporte alors deux diagonales. Les diagonales du pentagone le partage en onze
zones. |
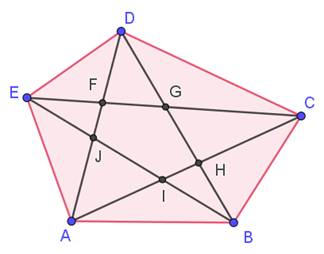
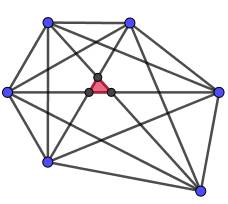
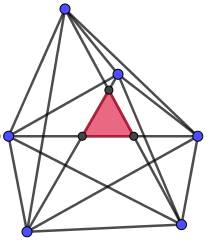
Pentagone quelconque, ses cinq
diagonales et leurs cinq points d'intersection
Matrice de connexions
|
|||
|
Exploitation de la matrice pour le
point A La matrice de connexion est recopiée dans un tableur
par exemple. Toutes les cases vides sont mises à 0, pour permettre le calcul
de la somme des 1 sur le tableau
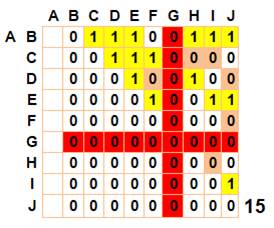
entier (outil "somme" du tableur). Ici, la somme vaut 15. Pour le travail sur le point A, on marque en
rouge les lignes et colonnes non reliées à A; ici le point G. Les valeurs
sont mises à 0. Avant de sommer, on vérifie les cas d'alignement:
Ne reste plus qu'à exécuter la somme pour obtenir
la contribution du point A. Exploitation pour les autres points |
Les 15 triangles à partir du point
A
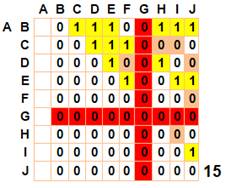
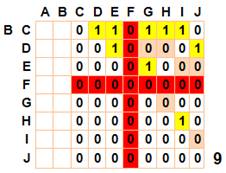
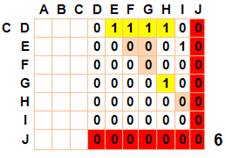
Le même procédé est appliqué aux autres points avec exclusion:
|
|||
|
|
|
|
||
Voir Triangles
dans l'hexagone
|
|
||||
|
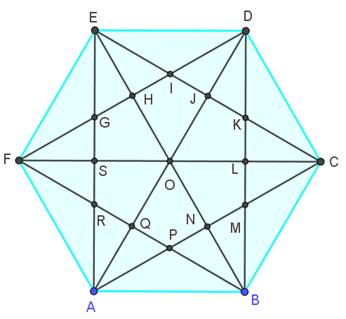
L'hexagone
régulier avec ses 9 diagonales et leurs 13 points d'intersection. Cette figure contient 110 triangles.
Valable pour:
Il faut ajouter un triangle
de plus pour:
|
Hexagone
régulier |
|||
|
Hexagone
semi-régulier |
Hexagone convexe |
Hexagone concave |
||
Quantité de points d'intersection
|
La quantité de points
d'intersection est facile à calculer pour un polygone convexe non-régulier
(pas de diagonales concourantes):
|
Pour l'hexagone:
|
Suite sur la page
externe indiquée en liens
|
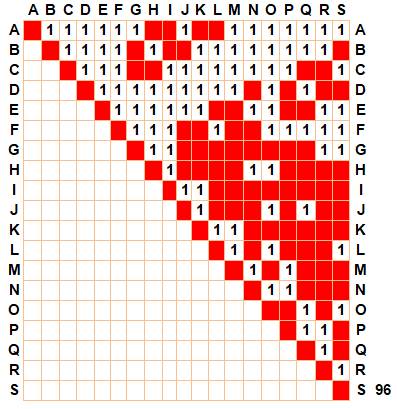
Matrice de connexions Les 1
indiquent les points reliés par un segment, comme AB, AC, AD, … Les carrés
rouges montrent que ces deux points ne sont pas reliés, comme A et H ou A et
I, etc. Conseil: pour suivre
les explications: utiliser l'outil capture pour disposer de la figure sous
les yeux. |
|
|
|
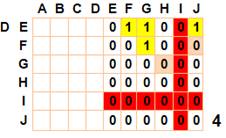
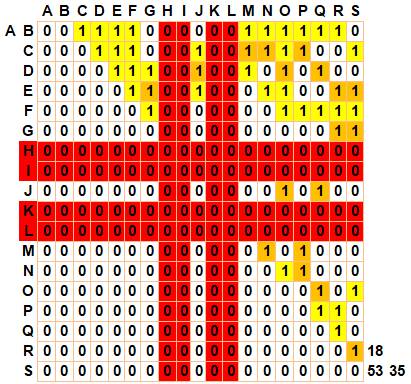
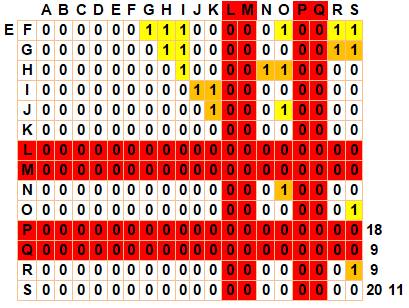
Les 35 triangles formés à partir du
sommet A La toute première colonne à
gauche indique le premier sommet (ici A). En rouge les exclusions
lorsque A n'est pas relié à ces points (H, I, J, K, l et S), en horizontal comme
en vertical. En ocre, les cas de points
alignés. Ils sont 18. En jaune les triangles à
retenir. Ainsi, la première case en jaune (haut-gauche) donne le triangle
ABC. Total: 53 x 1 – 18 alignements = 35. |
|
|
|
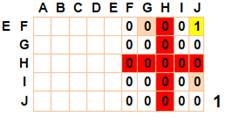
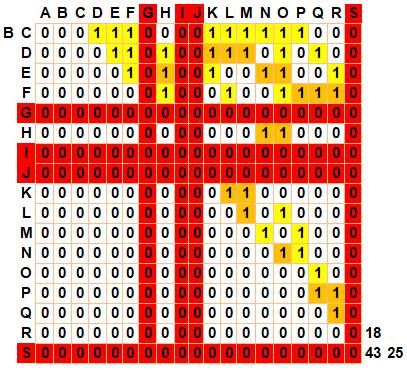
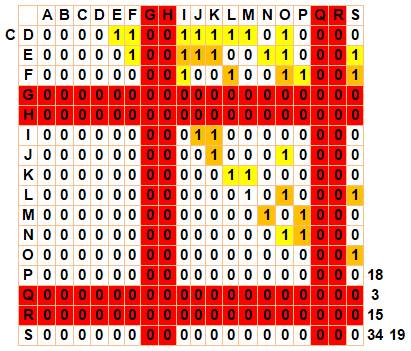
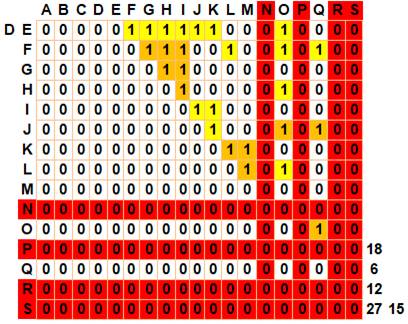
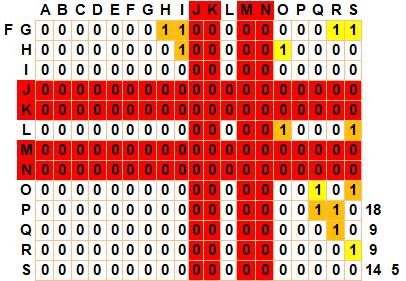
Analyse des points suivants
|
|
|
|
|
|
|
|
|
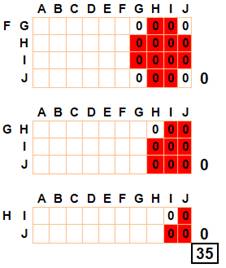
Les autres points de donnent pas de nouveaux triangles Total: 35 + 25 + 19 + 15 + 11 + 5 = 110 |
|
Voir Triangles
dans hexagone avec quelques diagonales
|
Cette méthode nécessite beaucoup de soin et une
vérification finale. Il est sans doute possible de la mettre sous forme de
programme. En fait, il existe une méthode de dénombrement (Voir The number of
triangles), mais elle est assez complexe, notamment pour éliminer les
faux triangles. |
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
|
|
|
Cette page |
http://villemin.gerard.free.fr/GeomLAV/Triangle/Particul/TrgPoly.htm
|
![]()