|
|||||||||||||||||||||||||||||||||||||
![]()
|
HEPTAGONE régulier Construction par neusis
La
construction de l'heptagone régulier avec règle et compas est impossible.
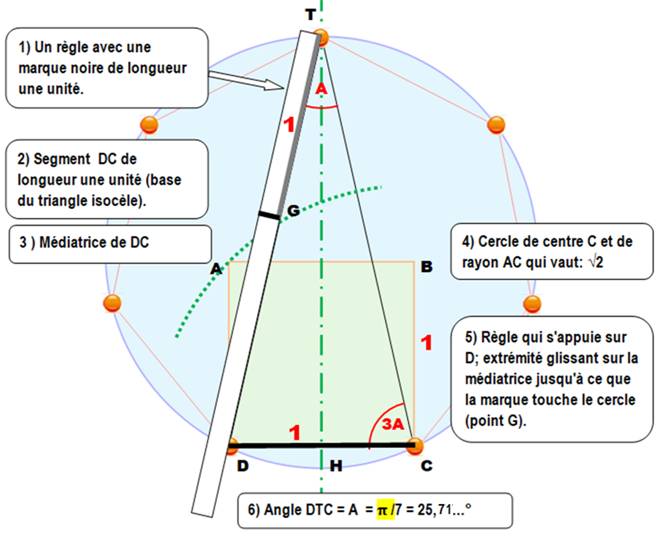
Par contre, elle est possible en déplaçant une règle marquée d'un trait.
C'est la méthode par neusis (du grec: pencher vers) utilisée dans l'Antiquité Trois
étapes pour montrer la construction de l'heptagone par neusis. |
Lignes trigonométriques de Pi/7
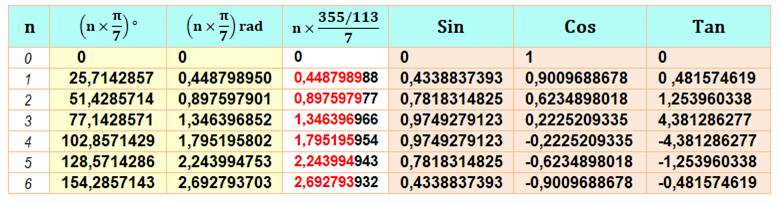
Voir Angles
en Pi / 7 / Calcul
du cosinus de Pi/7 /Trigonométrie
Rappel
|
La
calculette
de l'ordinateur offre une précision sur 32 chiffres
|
![]()
|
|
|
|
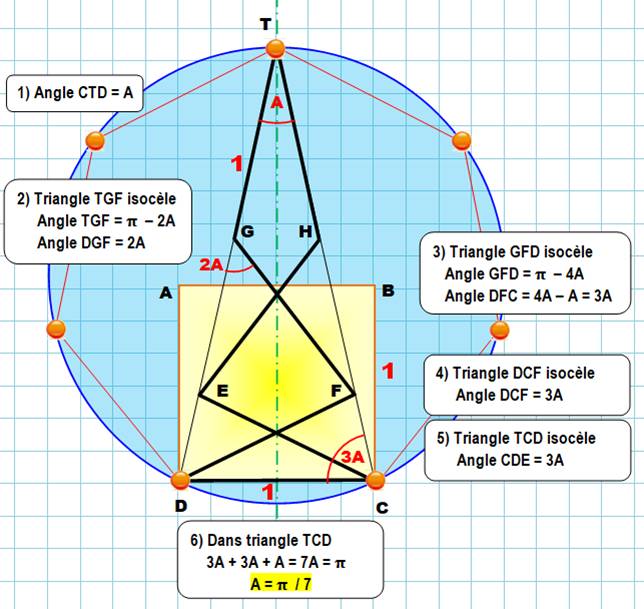
Prenez sept allumettes
identiques. Disposez-les comme sur la figure en alignant les extrémités sur
la même droite (chacun des deux côtés d'un triangle isocèle). La base du
triangle isocèle est bien constituée d'une allumette, elle aussi.. On va montrer que l'angle au sommet vaut: A = 25,71 ° = Note: la
construction est montrée en superposition du tracé final de l'heptagone et de
son cercle circonscrit pour référence.
|
|
|
|
||
|
Par rapport à la construction à la règle et au
compas, la construction par neusis autorise en plus une règle marquée, équivalent de
l'allumette utilisée ci-dessus. Dans ces conditions, les problèmes grecs insolubles deviennent faisables. Johnson en
1975 indique une construction de l'heptagone:
|
||
|
Calcul de CG Dans le triangle rectangle THC |
|
|
|
Résolution du triangle TGC |
|
|
Merci à Patrick H. pour sa lecture attentive
|
|
|
|
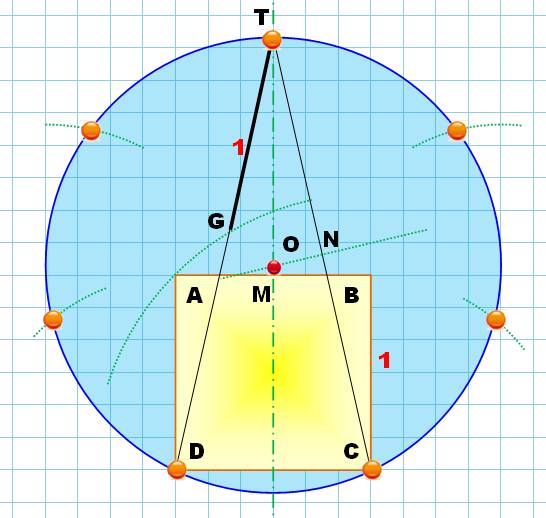
Avec la construction précédente, nous
obtenons le triangle isocèle TDC: (1; En traçant les médiatrices des côtés,
nous obtenons le point 0 centre du cercle circonscrit
de l'heptagone. Il suffit de reporter la distance DC sur le cercle pour obtenir les
quatre autres points.
|
|
Merci à Jelobreuil pour sa contribution à la
qualité de cette page
|
|
|||
|
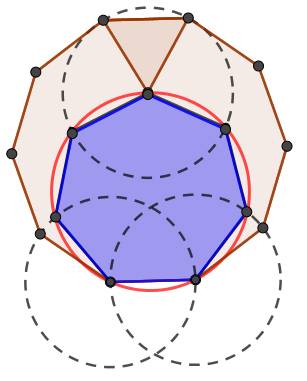
Par un
phénomène de coïncidence, il est possible de construire un heptagone à partir
d'un décagone.
La construction est presque parfaite. Cette construction est due à Jean-Louis Breuil. Construction Un décagone et un triangle équilatéral
construit sur un côté. Un cercle passant par le sommet de ce triangle et
par les extrémités du côté opposé. C'est le cercle circonscrit à l'heptagone
de même longueur que le côté du décagone. Des extrémités du côté opposé, deux cercles de
rayon égal au côté du décagone. Ils produisent deux intersections avec le
cercle précédent. Les segments joignant ces intersections aux
extrémités du côté constituent deux nouveaux côtés de l'heptagone. Un report
par compas permet de trouver les deux autres sommets. |
Construction
|
||
|
Approximation Un agrandissement au voisinage du sommet du
triangle équilatéral montre qu'il ne
se superpose pas avec le sommet de l'heptagone. L'erreur mesurée avec GeoGebra est de 2,12% Jean-Louis Breuil précise: L'erreur sur la
hauteur de l'heptagone est d'environ 1 % : si je prends le côté du dodécagone
pour unité, la hauteur calculée au moyen de la tangente de 3pi/7 vaut 4,3814, et celle calculée comme la différence
entre le double de l'apothème du décagone et la hauteur du triangle
équilatéral vaut 4,4233. Ce qui est
vraiment surprenant, c'est la presque parfaite coïncidence au niveau des
angles que révèle ma figure ! |
Détail
|
||
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Histoire/HeptaNeu.htm
|
![]()