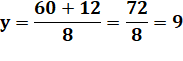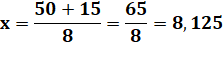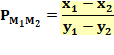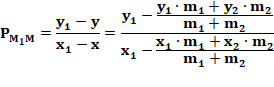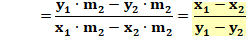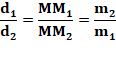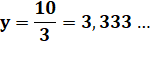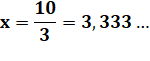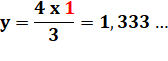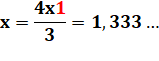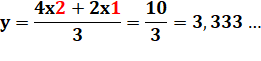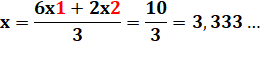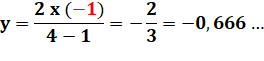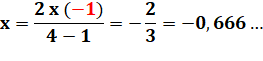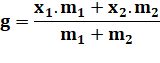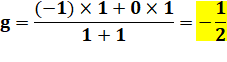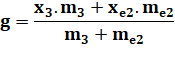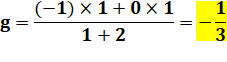NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 21/04/2020 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	PHYSIQUE
Débutants Base de la physique	Centre de Gravité			Glossaire Barycentre
INDEX Barycentre Géométrie Sciences	Débutant	Calcul	Forme simple	Multiforme
		Table	Forme complexe	Intégration
		Triangle	Trapèze	Demi-cercle
		Sommaire de cette page >>> Principe >>> Moment >>> Exemple de calcul >>> Trucs >>> Calcul de y avec l'axe de rotation x >>> Calcul de x avec l'axe de rotation y >>> Exemple de l'équerre – Diverses possibilités >>> Bilan – Formules de calcul >>> Cas de l'escalier >>> Empilement de dominos >>> Cas d'un profilé

Centre de Gravité

Principe du calcul

Nous allons nous intéresser à deux particules, chacune ayant une masse donnée. Le calcul fait intervenir une situation imaginaire mettant en jeu la pesanteur (gravité sur Terre).

Anglais: Torque or moment of force: tendency of a force to rotate an object about an axis.

Principe – Rotation potentielle
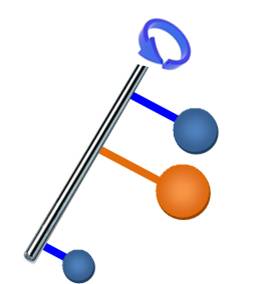
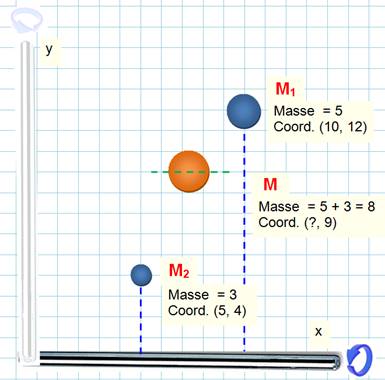
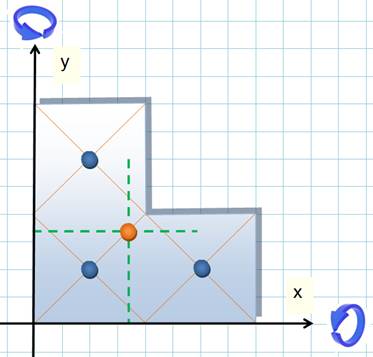
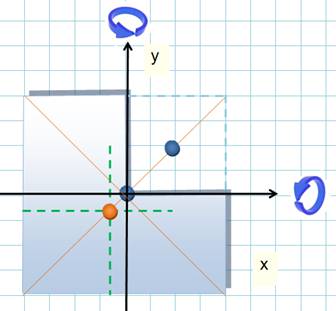
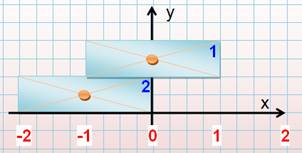
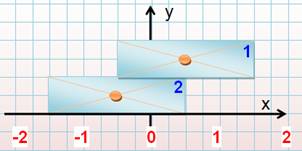
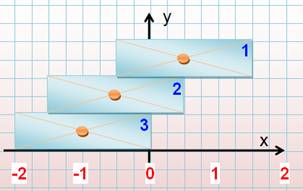
Soit un ensemble de points (bleus) de masses données fixées à un axe de rotation imaginaire et quelconque. Le centre de gravité des deux points est un point (marron) où serait concentrée toute la masse et qui aurait le même effet en termes de rotation. La masse équivalente est la somme des masses. Par contre, où se trouve le centre de gravité? Quelles sont ses coordonnées?	Quel le centre de gravité des particules bleue? Un point quelque part sur la particule marron. L'axe de rotation est là uniquement pour aider à faire le calcul.

Moment d'une force
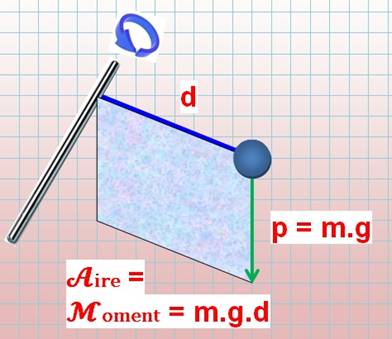
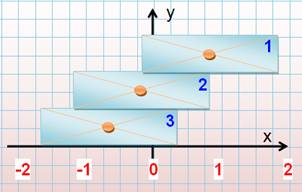
Pour caractériser l'effet potentiel de rotation, on fait appel au moment d'une force. Ici nous allons faire agir la force de gravité (le poids). L'effet de rotation est d'autant plus important que la masse est grande et, aussi, d'autant plus que le bras (de levier) est plus long.	Moment = poids x longueur du bras de levier = masse x accélération de la pesanteur x distance à l'axe de rotation = m . g . d
Vous pouvez imager cette définition en dessinant le rectangle dont l'un des côtés mesure la distance à l'axe et l'autre le poids. L'effet potentiel de rotation dû à cette particule est proportionnel à l'aire de ce rectangle.

Exemple de calcul
Deux masses ponctuelles sont situées comme indiqué. Quel est leur centre de gravité? Nous prenons les axes classiques d'un repère orthonormé comme axe de rotation. Par la pensée, imaginez que l'on tourne la figure pour que les masses deviennent pesantes et fassent tourner un des axes de rotation. Ces forces sont plus ou moins actives en fonction de leur distance à l'axe. En un mot, selon leur moment, le moment de chaque force par rapport à un des axes choisi agit. L'action résultante est la somme des deux actions, la somme des deux moments. Alors, le principe est de dire: qu'elle est la masse et son bras de levier tels que le moment soit égal à la somme des moments des deux forces?	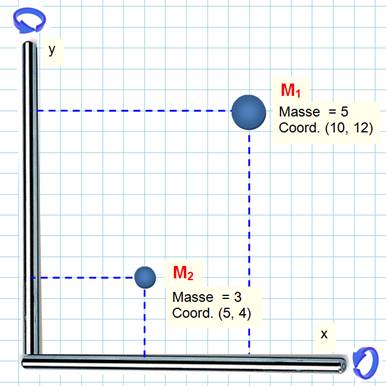Pour chaque axe: Moment total = moment de M1 + moment de M2

Quelques trucs à saisir!

Pour réaliser le calcul, on se place dans une situation imaginaire en faisant appel à la physique:

Les deux axes sont examinés chacun à leur tour: l'un pour calculer l'abscisse et l'autre l'ordonnée du centre de gravité.

Les masses sont au bout de tiges imaginaires raccordant les masses à l'axe.

L'axe choisi est positionné de façon telle que les masses sous l'effet de leur poids font tourner l'ensemble.

C'est le moment de chaque force qui caractérise l'aptitude de chaque masse à faire tourner l'ensemble.

Toutes les contributions sont ajoutées: somme des moments.

On cherche une masse unique qui aurait le même moment, le même effet de rotation.

Laissez-vous guider, le calcul est d'une redoutable simplicité …

Calcul de y avec l'axe de rotation en x
Pour l'axe x, quelle est l'ordonnée y du centre de gravité telle que la masse totale disposée en cet endroit produise le même effet, le même moment. Le moment cherché est la somme des moments par rapport à l'axe x. Lecture: le moment de la masse équivalente M par rapport à l'axe de rotation x est égal à la distance cherchée (y) multipliée par la masse totale (5 + 3) que nous égalons à la somme du moment de la première particule (M1) égale à sa distance (12) multipliée par la masse (5), plus le moment de M2 qui est égale à la distance (4) multipliée par la masse (3).

Oups! Que faites-vous de g?

Lors du calcul de y on a g en facteur au numérateur qui sera divisé par g au dénominateur. Simplification par g. On a introduit l'effet de la gravité pour mettre en place le calcul, mais finalement cette constante disparaît au cours des opérations.

Calcul de x avec l'axe de rotation en y
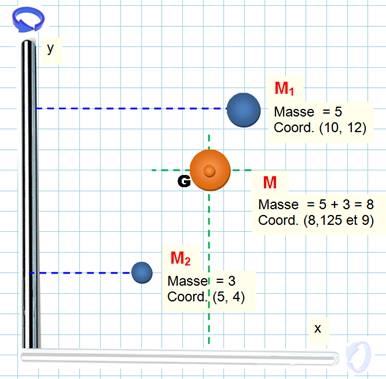
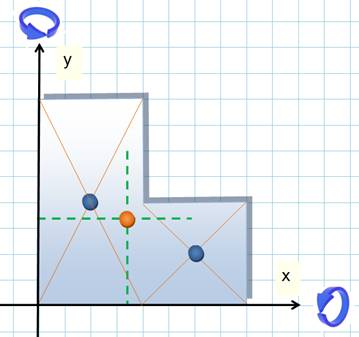
Le moment cherché est la somme des moments par rapport à l'axe y. Bilan: le centre de gravité se trouve en (x = 8,125 et y = 9) Remarque Les vecteurs M2M1 (5;8) et M2G (3,125;5) sont colinéaires puisque leur déterminant vaut 0. En effet: 5 x 5 – 8 x 3,125 = 0. Donc, les points sont alignés. Autre calcul ci-dessous.
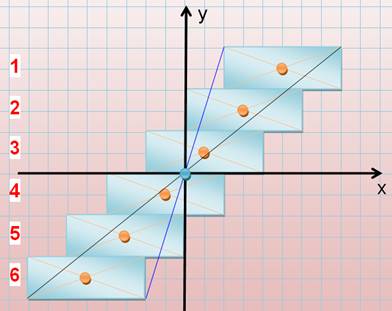
Alignement des trois points Les trois points (M1, M et M2) sont alignés. Calculons les pentes M1M2 et M1M:	Le point M se trouve sur la droite M1M2 en un lieu pondéré par le rapport des masses:

Merci à Yves Béraud pour cette observation sur l'alignement des points

Cas d'une équerre – Exploration des possibilités de calcul
Il s'agit d'une équerre homogène telle que dessinée. Chaque carré possède son centre de gravité. On représente chaque carré par une particule de masse équivalente en son centre de gravité (points bleus). Axe de rotation y Axe de rotation x En rouge, la valeur des "masses".
Système d'axes au choix Autant choisir le plus pratique.
On aurait pu se compliquer (un peu) la vie en prenant un rectangle et un carré
Encore un exemple illustratif qui montre comment retirer une pièce. Ici, on considère la plaque complète de 8 x 8, et on place les axes de rotation au centre de gravité de cette plaque Puis, on retire le coin haut à droite de 4 x 4.

Anglais: plaque ou lamelle => lamina

Bilan

Les coordonnées du centre de gravité se calculent

en choisissant deux axes qui semblent les plus sympathiques pour les calculs;

en calculant pour k particules de "masse" m_k et de coordonnées (x_k , y_k):

Un tel calcul avec les pondérations dues aux "masses" s'appelle un calcul de barycentre.

Théorème de Varignon

Soit une force F telle que .

Le moment de la force F par rapport à un point est égal à la somme des moments des forces F₁ et F₂ par rapport à ce même point.

Voir Varignon et contemporains

Cas de l'escalier
Nous avons vu l'exemple de l'escalier en première page. À première vue, cet objet semble bien symétrique et nous pensons que le centre de gravité est au centre géométrique, le point d'intersection des diagonales (bleues). Certes, mais c'est un escalier. Peut-être que ces zigzags changent les choses … Désormais nous disposons de la méthode pour situer le centre de gravité:
Nous dessinons le centre de gravité des six formes élémentaires. Ici, s'agissant de rectangles, il s'agit bien du centre géométrique (points orange). Ces six points de "masse" identique reflètent l'escalier complet. Nous calculons le barycentre de ces six points. Avec le système d'axes choisi, nous constatons que ces six points sont symétriques deux à deux. Les moments s'annulent pour chaque paire et pour chaque axe. Le centre de gravité est bien à l'origine des axes choisis (point bleu)

Cas de l'empilement des dominos
Domino de masse 1 et de longueur 2. Centre de gravité de ces deux dominos (1) et (2): Faisons glisser l'ensemble pour placer le centre de gravité sur l'axe y. L'ensemble des deux dominos est en équilibre avec son centre de gravité à la verticale de l'origine.
Plaçons un nouveau domino (3) sur l'axe x avec un coin en O; et posons dessus notre ensemble précédent, baptisé e2. Centre de gravité de ce nouvel ensemble: En faisant glisser l'ensemble vers la droite de 1/3 nous retrouvons un ensemble e3 en équilibre avec son centre de gravité à la verticale de O (sur l'axe y).
Vous l'avez compris, en répétant cette procédure de glissement de 1/2, puis1/3, puis 1/4, puis … nous conservons l'équilibre. Intuitivement cette construction ne demande qu'à tomber. Pourtant nous venons de démontrer que l'équilibre est maintenu à chaque fois que l'on ajoute un domino en le glissant d'un pas mesurant 1/k.

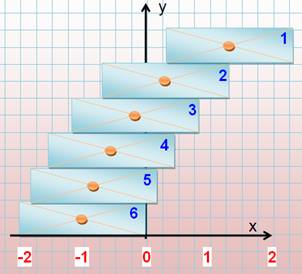
Voir Paradoxe de la tour penchée et suite harmonique / Dominos

Cas d'un profilé
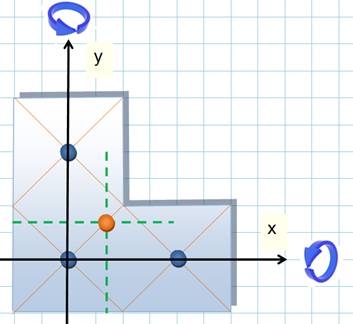
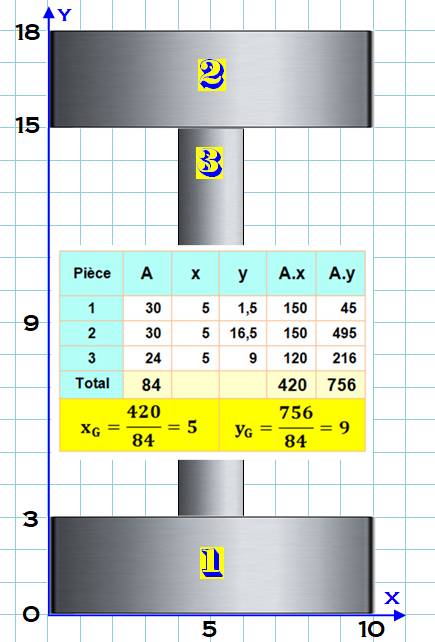
Cette forme possède deux axes de symétrie: la droite x = 5 et la droite y = 9. Le centre de gravité est en xG = 5 et yG = 9. Bien! Mais voyons le calcul pour voir comment s'y prendre dans un cas plus complexe. Le tableau indiqué est une forme bien pratique pour identifier chaque composante (1, 2 et 3) et les données correspondantes: A = aire de la composante, x et y les coordonnées de leur centre de gravité. On calcule les moments A.x et A.y qui sont sommés, puis divisés par l'aire totale pour donner les coordonnées du centre de gravité de l'ensemble.

Voir Poutres / Forces dans les constructions

Suite	Centre de gravité – Formes simples Centre de gravité et barycentre – Glossaire Calcul du centre de gravité avec les nombres complexes
Voir	Archimède – Biographie Euréka Forces Histoire Multiplication Sciences – Index Treuil
Aussi	Gravité dans DicoMot
Livre	Architecture et construction – Enseignement technologique de première et terminale (STI2D) – Aksel Kaptan – ellipses – 2017
Cette page	http://villemin.gerard.free.fr/aScience/Physique/STATIQUE/CGMoment.htm