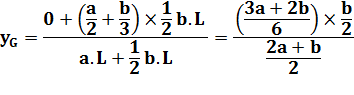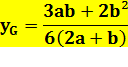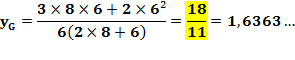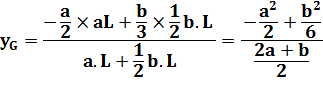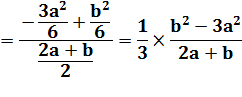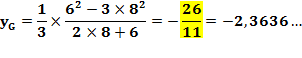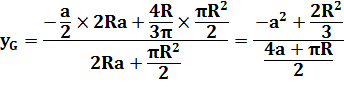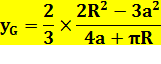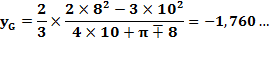NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 16/06/2014 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique
	PHYSIQUE
Débutants Base de la physique	Centre de Gravité			Glossaire Barycentre
INDEX Barycentre Géométrie Sciences	Débutant	Calcul	Forme simple	Multiforme
		Table	Forme complexe	Intégration
		Triangle	Trapèze	Demi-cercle
		Sommaire de cette page >>> Enveloppe ou maison >>> Porte en arceau >>> Triptyque

Centre de gravité de figures multiformes

Exemples de calculs et méthodes de vérification.

Au préalable lire: Méthode générale de calcul en utilisant les moments

Enveloppe ou maison
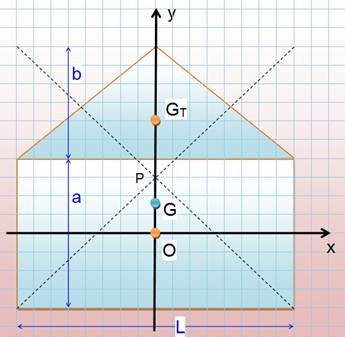
Calcul 1) Rectangle: Le centre de gravité est en O: GR (0,0); Aire: a . L Triangle: Centre de gravité est au 2/3: GT (0, a/2 + b/3) Aire: ½ b . L Centre de gravité cf. Symétrie de la figure	Le point G est un peu en dessous de P, le centre de gravité du rectangle enveloppe. Application numérique
Calcul 2) pour confirmation Rectangle: Centre gravité: GR (0,-a/2); Aire: a . L Triangle: Centre de gravité est au 2/3: GT (0, b/3) Aire: ½ b . L Centre de gravité cf. Symétrie de la figure	Application numérique Nous vérifions que 18/11 + 26/11 = 44/11 = 4.

Porte en arceau
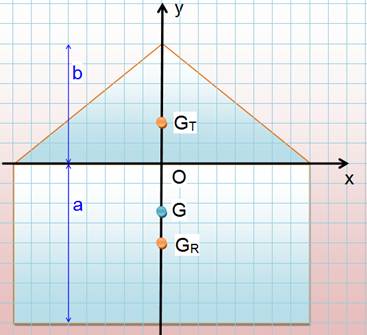
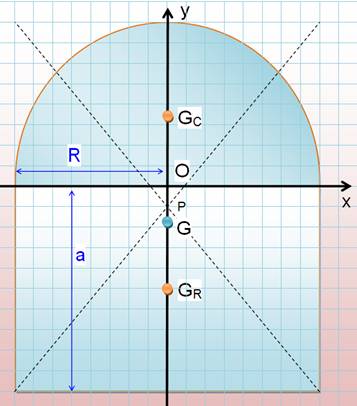
Rectangle: Le centre de gravité est en O: GR (0,-a/2); Aire: 2R . a Cercle: Centre de gravité: GT (0, 4R/3) Aire: ½ R² Centre de gravité cf. Symétrie de la figure	Le point G est légèrement en dessous de P, le centre de gravité du rectangle enveloppe. Application numérique

Triptyque
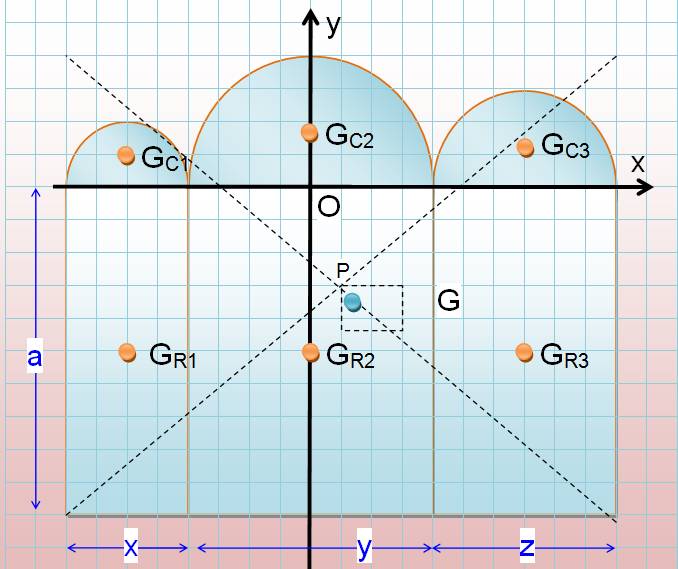
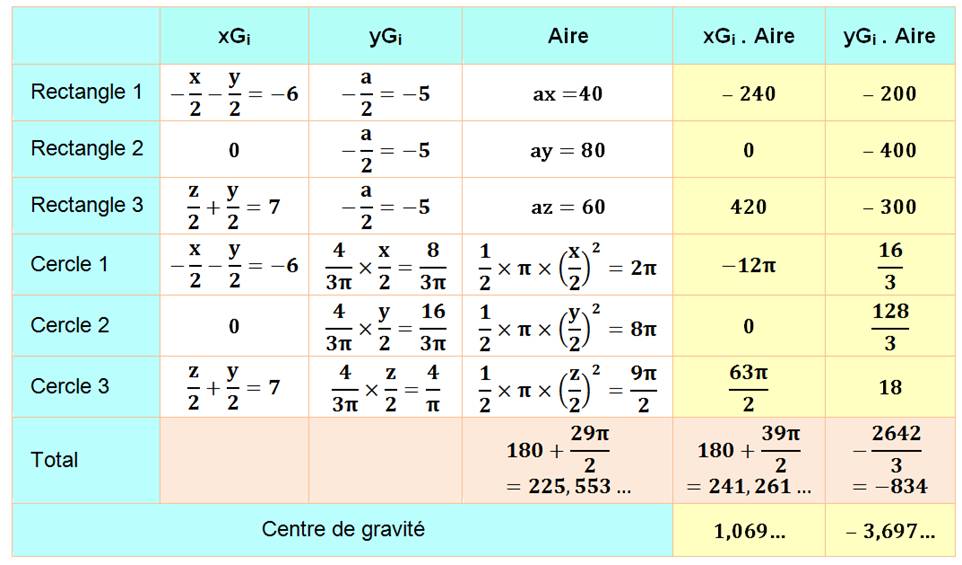
Exemple de calcul complexe avec disposition des calculs en tableau. On passe rapidement aux valeurs numériques. Une formule littérale pour ce genre de figure n'a pas beaucoup de sens. Le point G est légèrement en dessous et à droite de P, le centre de gravité du rectangle enveloppe. Il est sans doute dans le rectangle dessiné en pointillés.

Suite	Centre de gravité – Tables récapitulatives Centre de gravité et barycentre – Glossaire
Voir	Archimède – Biographie Euréka Forces Histoire Multiplication Sciences – Index Treuil
Aussi	Gravité dans DicoMot
Cette page	http://villemin.gerard.free.fr/aScience/Physique/STATIQUE/CGFormMu.htm