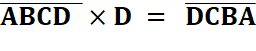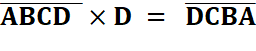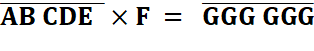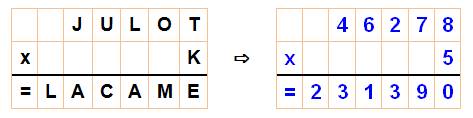![]()
|
|
Ce site est désormais accessible en http://diconombre.fr/index.html et
pour cette page voir le lien en fin de page For
this page, refer to the link at the bottom. |
|
22 Novembre 2025
![]()
|
|||||||||||||||||||||||||||||||||||||||||||||
![]()
|
PUZZLES
ARITHMÉTIQUES Cryptarithmes – Cryptogrammes MULTIPLICATIONS |
Devinettes
|
Défi 1: trouvez la valeur des lettres toutes
différentes telles que:
1 089 x
9 =
9 801 Voir Autres du genre par
retournement Défi 2: trouvez la valeur des lettres toutes
différentes telles que:
|
Voir
Palindromes / Solution du défi 2 / Défi OUI² = OOUUI
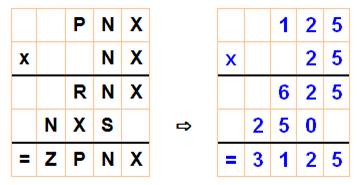
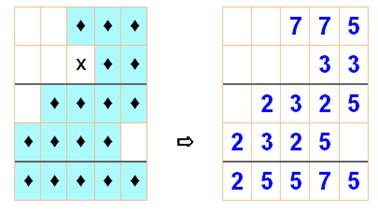
Un cas typique avec une croix
en 5

Voir Multiplications
|
|
||
|
|
|
|
|
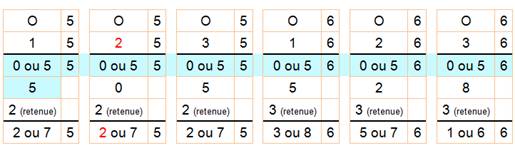
Dernière
colonne: |
X
. X donne X X
= 0, 1, 5 ou 6 |
|
|
3e ligne => X . PNX = RNX: |
X
= 0 => 0 . PNX = XXX Non X
= 1 => 1 . PNX = PNX Non X
= 6 => 6 . PN6 = PN6
N'existe pas X
= 5 => 5 |
|
|
Possibilités: |
N
= 2 ou 7 5
x 25 = 125 ou 5 x 75 = 375 |
|
|
Situation |
|
|
|
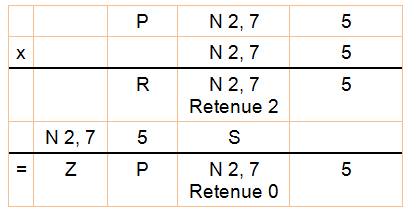
Examinons PN5 x N: |
Si
N = 7 P75
x 7 => se termine par 5 S
= 5 Ce
qui n'est pas possible (5 déjà utilisé) Donc:
N = 7 |
|
|
Situation |
|
|
|
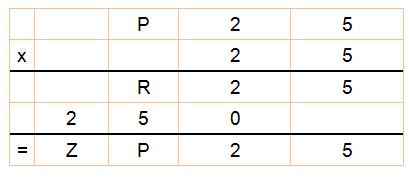
Examinons P25 x 2: |
P25
x 2 = 250 P
= 1 |
|
|
L'opération est connue: |
R
= 6 Z
= 3 |
|
|
|
||
|
|
|
|
|
N a 4 chiffres |
C
. C ne donne pas de retenue donc C < 4, soit 1, 2 ou 3. |
|
|
M a 5 chiffres |
U
. C > 9 avec C < 4 => U n'est pas 1. |
|
|
P tel que U . U => U |
U
= 5 ou 6 (5² = 25 et 6² = 36). |
|
|
Bilan |
U
= 5 ou 6; C = 1, 2 ou 3. Soit six possibilités. |
|
|
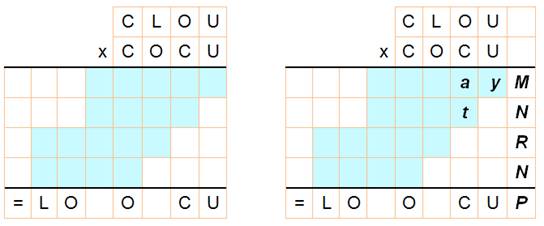
Posons les mini
opérations Seule la deuxième
donne la possibilité de voir C apparaitre en bas |
|
|
|
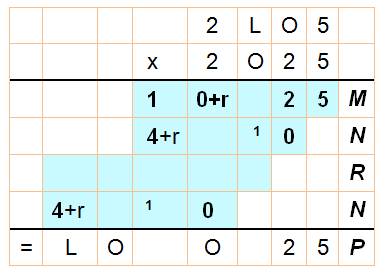
Bilan U = 5 et C = 2 2x5 = 10 => t =
0 a + t = 2 => a =
2 => O est pair En N: L > 4 |
|
|
|
R = O x 2LO5 |
Or R dépasse les 10 000 => O > 5 soit 6 ou 8. |
|
|
Sachant que {0, 1,
2, 5} sont déjà utilisés, que O est pair et que L > 4 |
Si O = 4
=> L ={6, 7, 8, 9} Si O = 6
=> L ={7, 8, 9} Si O = 8
=> L ={6, 7, 9} |
|
|
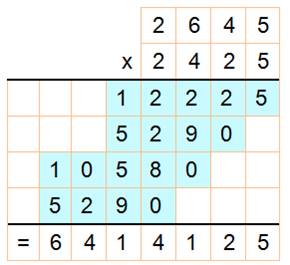
Après quelques
essais avec ces valeurs, la solution est: |
|
|
Librement repris d'après Jean Pierre Alem
|
|
||
|
|
|
|
|
|
||
|
|
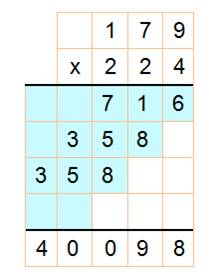
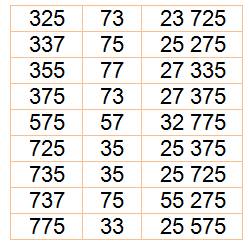
Problème et une des solutions
Les neuf solutions
|
|
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Cette page |
![]()