pem NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 24/01/2017 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique
	RUBRIQUE Nombres
Débutants Général	Formes retournées			Glossaire Général
	Général	Opérations palindromes	Séquences
	Proportions	Premiers	Division
	Sommaire de cette page >>> Anatomie du motif >>> Nombres divisibles par m et son retourné >>> Famille du nombre 84 >>> Nombres divisibles simultanément par m et son retourné >>> Motifs infinis >>> Nombres doublement retournés

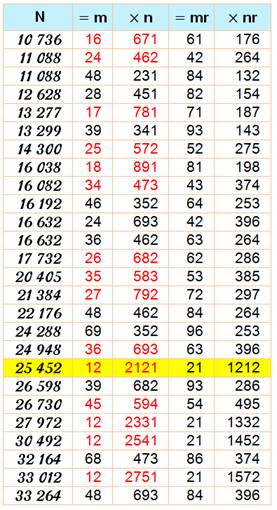
Nombres retournés

et division

Trouver les nombres N divisibles à la fois par m et par son retourné mr (4321 et le retourné de 1234).

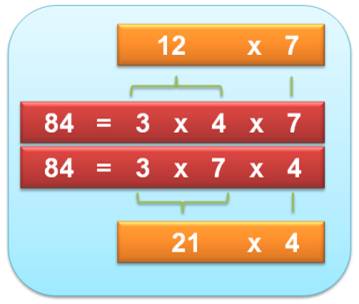
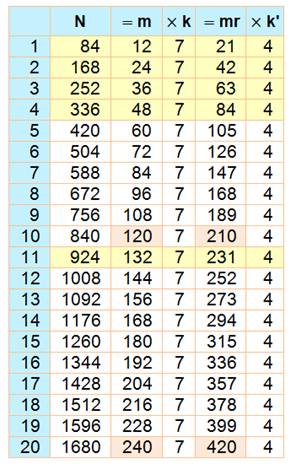
Par exemple, 84 est divisible par 12 et par 21, et c'est le seul nombre à deux chiffres. Extraordinaire! Son double 168 est divisible par 24 et par 42 …

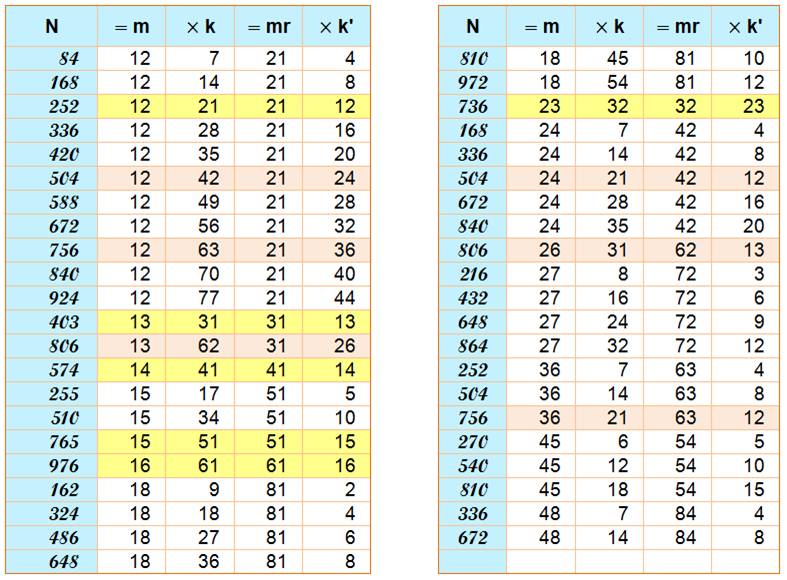
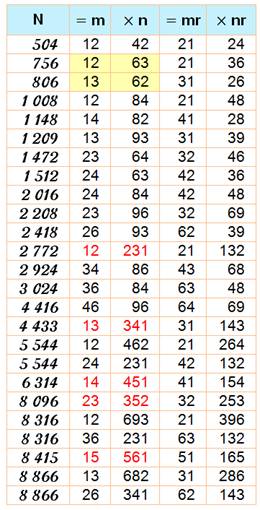
Nous ferons connaissance aussi avec les doublement-retournés comme 504 = 12 x 42 = 21 x 24.

Anatomie du motif
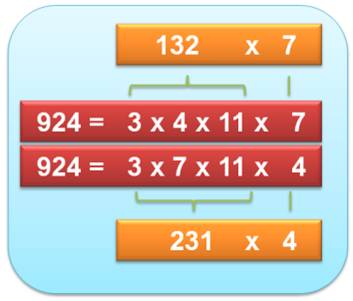
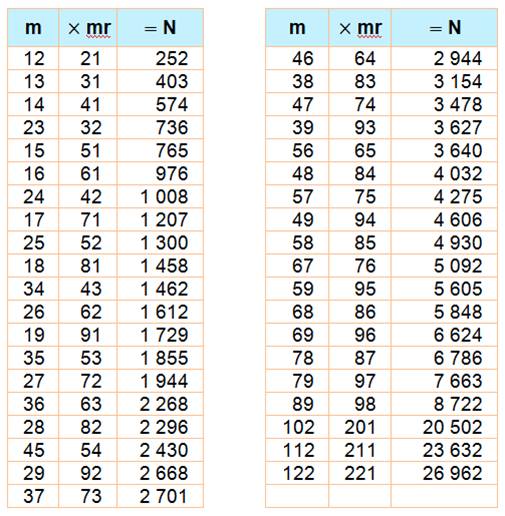
Nous cherchons les nombres N divisible à la fois par un nombre m et son retourné mr. Exemples: les seuls tels nombres divisibles par un nombre de deux et trois chiffres sont 84 et 924. En développant 84 et 924 en leurs facteurs, le motif apparaît clairement. Pour passer de 84 à 924, il suffit de multiplier le motif par 11.

Voir Famille de 84

Nombres divisibles par m et son retourné
Pour N jusqu'à 1000 et avec deux chiffres pour m, ils sont 43: En jaune: les nombres déjà produit de deux facteurs retournés. En rose: les nombres doublement retournés par leur diviseur et leur quotient.

De 1000 à 10 000 avec m à 3 chiffres, ils sont 52:

Voir Nombres somme de m et de son retourné

Famille du nombre 84
Le nombre 84, par exemple, est à la tête d'une famille. Les multiples sont aussi divisibles par le retourné: 84k = 12 x 7k = 21 x 4k. Par contre, les motifs deviennent rares si m est remplacé par k m : seuls cinq cas se distinguent (jaune). Les cas en rose sont de presque-motifs (multiples en 10 du motif de départ).

Nombres divisibles simultanément par m et mr
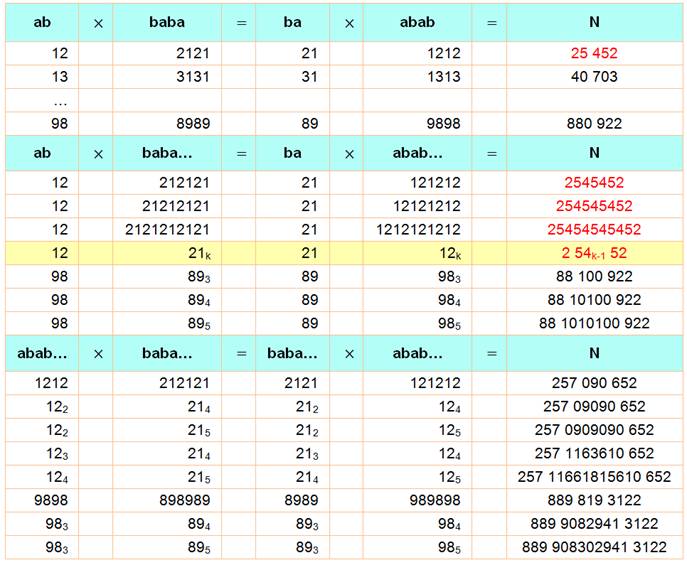
Les nombres N divisibles par m et mr sont tous les nombres, produits des m et mr successifs. Une sorte de pseudo-carré. On retire de la liste les carrés des repdigits comme 11 x 11 = 121. Ces nombres sont magiques car ils forment des motifs infinis

Motifs infinis avec les retournés
Les nombres en N = 10a + b (noté ab) et leur retourné Nr = 10b + a (noté ba) forment des motifs infinis en répétant et en multipliant. Ce tableau montre des exemples en début de liste (12) et en fin de liste (98). Aucun n'engendre de retenues détruisant l'égalité. Avec 12 et 21 le produit est toujours palindrome (rouge), dont on donne la formule générique (ligne en jaune).

Voir Pépites numériques

Nombres doublement retournés
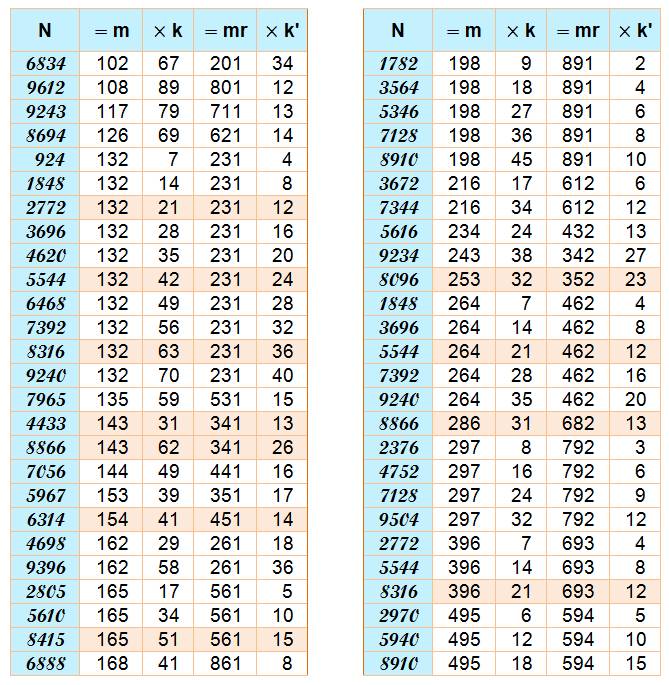
Les nombres N divisibles par m et n et par leur retourné. Il y en a sans doute une infinité. 504 est le plus petit motif. C'est 2772, le plus petit comportant un nombre à trois chiffres. C'est, en plus, un palindrome. Les quatre marqués en jaune clair sont très proches avec 12, 13 et 62, 63. En rouge les chiffres de m sont dans n. Le nombre palindrome 25 452 (ligne en jaune) est remarquable!	Exemple pour les deux au-dessus du million

Voir 2016

Suite	Formes retournées en général Nombres permutés Puissances de 2 retournées
Voir	Chiffres en miroir Factorielle Motifs Multiplication ABCDE = F x GGGGGG Nombres de Friedman Nombres en 4 fois 4 Procédé de Kaprekar Puissance Puzzles – Index Tables – Index
DicoNombre	Nombre 84 Nombre 252 Nombre 504 Nombre 924 Nombre 1089 et magie Nombre 2 772 Nombre 3 003 Nombre 25 452 Accès aux autres nombres
Site	Math is fun forum (anglais)
Cette page	http://villemin.gerard.free.fr/aNombre/MOTIF/RetDiv.htm