Nombres strobogrammatiques ou renversés

NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 11/04/2022 Orientation générale DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Nombres
Débutants Général	Formes retournées				Glossaire Général
INDEX Nombres	Général		Opérations palindromes	Séquences
	Proportions		Premiers	Division
	Puissances		Carré magique	Différence de carrés
	Strobogrammatique		Magie renversante	Premiers de Luhn
	Palintiple		Nombres qui se lisent	Palindromes
		Sommaire de cette page >>> Table des nombres de 1 à 999 >>> Nombres strobogrammatiques >>> Nombres strobogrammatiques premiers >>> Nombres tétradiques >>> Nombres dihédraux

SNCF et ses TGV

Le mot inouï en lettre rondes est lisible des deux côtés de la table (rotation de 180°).

La SNCF en a fait le logo des TGV.

Étymologie: qu'on n'a pas ouï, pas entendu.

Nombres Strobogrammatiques

ou ambigrammes

ou renversés

ou tétradriques

Nombres qui se lisent aussi bien même si la tablette (l'ardoise) est tenue à l'envers. Autrement-dit: c'est le même nombre après une rotation de 180°.

C'est le cas du nombre premier 619.

Anglais: strobogrammatic numbers or ambigram numbers

Table des nombres de 1 à 999 qui se lisent aussi bien en retournant le tableau (180°)

Voir Tables

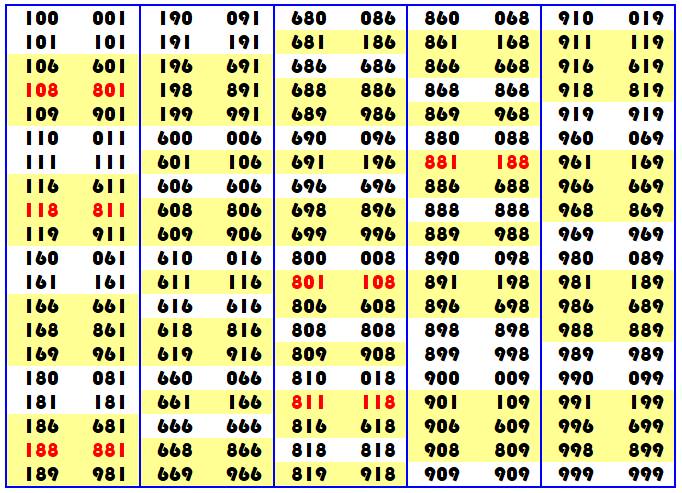
Nombres strobogrammatiques
Liste de tels nombres. Ils profitent: de la symétrie des chiffres: 0, 1 et 8 et de la possibilité d'échanger le 6 et le 9. Le chiffre 1 s'entend écrit en forme bâton, sans la petite barre initiale.	0, 1, 8, 11, 69, 88, 96, 101, 111, 181, 609, 619, 689, 808, 818, 888, 906, 916, 986, 1 001, 1 111, 1 691, 1 881, 1 961, 6 009, 6 119, 6 699, 6 889, 6 969, 8 008, 8 118, 8 698, 8 888, 8 968, 9 006, 9 116, 9 696, 9 886, 9 966, ...
Liste des nombres strobogrammatiques premiers.	11, 101, 181, 619, 16 091, 18 181, 19 861, 61 819, 116911, 119 611, 160 091, 169 691, 191 161, 196 961, 686 989, 688 889, 1 008 001, 1 068 901, 1 160 911, 1 180 811, 1 190 611, 1 191 611, 1 681 891, 1 690 691, 1 880 881, 1 881 881, 1 898 681, 1 908 061, 1 960 961, 1 990 661, …

Nombres tétradiques
Un nombre tétradique est un nombre palindrome avec symétrie horizontale, symétrie verticale et symétrie centrale Son écriture reste inchangée si l’on retourne le nombre de 180°. Les chiffres qui composent ce genre de nombres se limitent nécessairement à 0, 8 et 1 (seul chiffre impair)." Tétradrique: du grec tétras, quatre façons.			Ce sont les nombres strobogrammatiques dont on retire ceux comportant des 6 ou des 9.
Nombres tétradiques premiers. Tous se terminent par 1, évidemment.	11 101 181 18 181 1 008 001 1 180 811	1 880 881 1 881 881 100 111 001 100 888 001 108 101 801		110 111 011 111 010 111 111 181 111 118 818 811 180 101 081
Le plus grand nombre tétradique premier recensé en mai 2016 s’écrit en répétant le motif 1 808 010 808 mille cinq cent soixante fois, et en concaténant le chiffre 1 à la fin. Ce « petit » bijou a été découvert par les mathématiciens David Dubner et Harvey Broadhurst.

Anglais: tetradic numbers / tetradic primes

Source Tangente

Nombres dihédraux
Définition Nombres qui restent lisibles (sur un afficheur sept segments) dans un miroir ou en retournant le cadran (de la calculette), directement ou dans un miroir. Deux types les parfaits qui conservent la même valeur et les autres qui changent de valeur.			Les chiffres et leurs propriétés dihédrales Seuls 0, 1, 2, 5, 8 sont dihédraux.
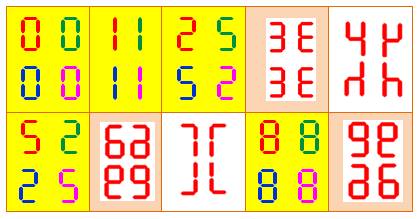
Exemples de dihédraux à quatre valeurs
Liste des dihédraux Retirer les nombres avec 2 et 5 pour obtenir les parfaits		0, 1, 2, 5, 8, 10, 11, 12, 15, 18, 20, 21, 22, 25, 28, 50, 51, 52, 55, 58, 80, 81, 82, 85, 88, 100, 101, 102, 105, 108, 110, 111, 112, 115, 118, 120, 121, 122, 125, 128, 150, 151, 152, 155, 158, 180, 181, 182, 185, 188, 200, 201, 202, 205, 208, 210, 211, 212, 215, 218, 220, 221, 222, 225, 228, 250, 251, 252, 255, 258, 280, 281, 282, 285, 288, 500, 501, 502, 505, 508, 510, 511, 512, 515, 518, 520, 521, 522, 525, 528, 550, 551, 552, 555, 558, 580, 581, 582, 585, 588, 800, 801, 802, 805, 808, 810, 811, 812, 815, 818, 820, 821, 822, 825, 828, 850, 851, 852, 855, 858, 880, 881, 882, 885, 888, 1000, 1001, …
Dihédraux premiers		2, 5, 11, 101, 151, 181, 211, 251, 281, 521, 811, 821, 881, 1021, 1051, 1151, 1181, 1201, 1511, 1801, 1811, 2011, 2081, 2111, 2221, 2251, 2281, 2521, 2551, 2801, 2851, 5011, 5021, 5051, 5081, 5101, 5281, 5501, 5521, 5581, 5801, 5821, 5851, 5881, 8011, 8081, 8101, 8111, 8221, 8501, 8521, 8581, 8821, …
Dihédraux premiers y compris leurs trois images		2, 5, 11, 101, 181, 1181, 1811, 18181, 108881, 110881, 118081, 120121, 121021, 121151, 150151, 151051, 151121, 180181, 180811, 181081, 188011, 188801, 1008001, 1022201, 1028011, 1055501, 1058011, 1082801, 1085801, 1088081, …
DIhédraux premiers et palindromes	2, 5, 11, 101, 151, 181, 10501, 12821, 15551, 18181, 1008001, 1022201, 1028201, 1055501, 1082801, 1085801, 1120211, 1150511, 1180811, 1201021, 1208021, 1212121, 1215121, 1218121, 1221221, 1250521, 1280821, 1281821, 1508051, 1520251, 1550551, 1551551, 1580851, 1802081, 1805081, 1820281, 1851581, 1880881, 1881881, …
Dihédraux parfaits, premiers et palindromes	2, 5, 11, 101, 181, 18 181, 1008001, 1022201, 1055501, 1082801, 1085801, 1180811, 1208021, 1221221, 1250521, 1280821, 1508051, 1520251, …