|
||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
NOMBRES PREMIERS en progression arithmétique Quels
sont les nombres
premiers à égale distance les uns des autres. Quelle est la chaine la
plus longue. Parmi le
premier million
de nombres premiers, il est facile de trouver une suite de 6 nombres en progression
arithmétique, et difficilement plus. Objectif
fou: comparaison d'une suite erratique de nombres (les premiers) et une suite
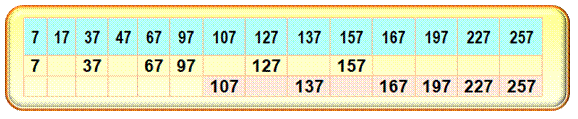
bien régulière (progression arithmétique) ! Exemple: deux suites de nombres premiers en 7, espacés de 30. En bleu tous les nombres premiers; en jaune la première suite et en
rose la seconde.
Voir Nombres
premiers avec 7 pour unité / Nombres premiers
équilibrés |
Types de
progression arithmétique
|
Progression
arithmétique (PA) de nombres premiers: dans tous les cas la différence entre
deux nombres premiers voisins est constante, et en plus:
Types de records des PA fortes:
|
|
|
||
|
La raison de
la progression arithmétique est la distance entre chaque nombre. |
3, 13, 23 sont trois nombres premiers espacés de 10. La raison est égale à 10. La différence
entre deux nombre voisins est égale à 10. |
|
|
Quelles
sont les valeurs possibles pour cette raison. Les
nombres premiers sont tous de la forme 6 En
partant de ces deux valeurs et en les additionnant plusieurs fois, on trouve la liste
indiquée. Cependant,
il faut exclure les nombres impairs,
car la somme suivant sera paire et donc composée. En effet: tous les premiers
(sauf 2) sont impairs et la somme (impair + impair) est paire. |
Liste des raisons possibles pour la progression
arithmétique entre les nombres premiers: 5, 7, 10, 12, 14, 20, 22, 24,
puis tous les nombres pairs suivants. Sont exclus, les nombres: 1, 2, 3, 4,
6, 8, 9, 11, 13, 16, 18 et 23. Cas particuliers avec R = 2 ou 4 pour 3, 5, 7 et 3, 7, 11 |
|
Voir Énigmes de
pesée
|
|
||||||
|
R indique
la raison; Dans la
colonne suite, on montre les premier, deuxième et dernier nombres de la
progression; et K,
indique la quantité de nombre de la progression. |
||||||
|
R |
Suite de premiers |
K |
R |
Suite de premiers |
K |
|
|
5 |
2, 7 |
2 |
36 |
31,
67, 103, 139 |
4 |
|
|
7 |
/ |
0 |
|
241,
277, 313, 349 |
|
|
|
10 |
3,
13, 23 |
3 |
|
… |
|
|
|
12 |
5,
17, 29, 41, 53 |
5 |
40 |
3,
43, 83 |
3 |
|
|
14 |
3,
17, 31 |
3 |
50 |
3,
53, 103 |
3 |
|
|
|
3, 23,
43 |
|
42 |
5,
47, …131 |
5 |
|
|
20 |
3,
23, 43 |
3 |
|
5,
47, …173 |
|
|
|
22 |
7, 29 |
2 |
|
… |
|
|
|
|
19,41 |
|
60 |
11,
71, …311 |
6 |
|
|
|
… |
|
|
53,
113, …353 |
|
|
|
24 |
59,
83, 107, 131 |
4 |
|
641,
701, …941 |
|
|
|
|
79,
103, 127, 151 |
|
|
5443,
5503, …5743 |
|
|
|
|
… |
|
90 |
13,
103, …463 |
|
|
|
30 |
7,
37, …157 |
6 |
|
503,
593 …953 |
6 |
|
|
|
107,
137, …257 |
|
|
|
|
|
|
|
359,
389, …509 |
|
|
|
|
|
|
|
541,
571, …691 |
|
210 |
199, 409,
619, 829, 1039, 1249, 1459, 1669, 1879, 2089 |
10 |
|
|
|
2221,
2251, …2371 |
|
|
|
|
|
|
|
6673,
6703, …6823 |
|
|
|
|
|
|
|
7457,
7487, …7607 |
|
|
|
|
|
|
|
||
|
Les progressions
arithmétiques sont notées (k, r) avec k la quantité de termes et r la raison
de la progression. |
Plus petites PA fortes (3, 2) => 3, 5, 7 (4, 6) => 251, 257, 263, 269 (5, 30) => 9 843 019, 9 843 049, 9 843 079, 9 843 109, 9 843 139 (5, 30) => 121 174 811, 121 174 841, 121 174 871, 121 174 901, 121
174 931, 121 174 961 Tous les premiers de ces progressions sont consécutifs. |
|
|
|
|
|
Infinité de nombres
premiers en progression arithmétique Adrien-Marie Legendre (1752-1833) conjecture
une infinité de nombres premiers pour les progressions
arithmétiques dont la raison et le premier terme sont premiers entre eux. Parmi les termes
de la progression certains sont composés. Johann Dirichlet (1805-1859) démontre ce
théorème en 1837. Hardy et Littlewood conjecturent en 1923
qu'il existe une infinité de progressions arithmétiques longues de premiers
(en fait, une conjecture plus large à propos des constellations
de premiers). Van der Corput prouve en 1939 qu'il
existe une infinité de triplets premiers en progression arithmétique. En 981,
Health-Brown montre qu'il existe une infinité de quadruplets avec
éventuellement l'un d'eux comme semi-premier. Ben Green et Terence Tao démontrent
en 2004 qu'il existe des chaines en progression arithmétiques aussi longue
que l'on veut. Théorème de Green-Tao
(2004) Il existe des progressions arithmétiques de nombres premiers arbitrairement longues. Voir Terence Tao La démonstration dit que l'on peut
trouver une progression arithmétique de longueur k pour tout k, mais ne dit
pas comment la construire. Exemple de très grande
chaine en progression arithmétique X = 1,009
… 1092
= 100 99697 24697 14247 63778 66555 87969 84032 95093 24689 19004 18036 03417 75890 43417 03348 88215 90672 29719 X + k. 210
: avec k = 0, 1, 2, ... , 9 sont tous premiers. Pour 10 nombres
successifs Calculés en mars 1998, il a fallu
200 ordinateurs, 70 mathématiciens impliqués. Ils ont 93 chiffres et sont
espacés de 210 en 210. En 2010, Benoît Périchon découvre
une suite de 26 premiers commençant par: C'est toujours le plus grand connu
en 2018. En 2018, on connait un nombre de 7
036 chiffres formant une progression de 7 termes (Auteur: Ken Davis). |
|
![]()
|
Voir |
|
|
Aussi |
|
|
DicoNombre |
|
|
|
|
|
Cette page |
![]()