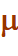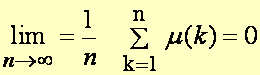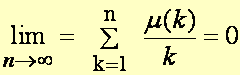NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 31/01/2023 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Nombres premiers
Débutants Identité d'Euler	Répartition			Glossaire Nombres premiers
INDEX Nombres premiers	En bref	Identité d'Euler	Fonction zêta d'Euler	F. de Möbius
	Débutant	Démo. de l'identité	Zêta de Riemann
		Approches modernes	Hypothèse de Riemann
		Sommaire de cette page >>> Fonction de Möbius >>> Valeurs >>> Fonction de Mertens >>> Valeurs >>> Conjecture de Mertens >>> Utilisation >>> Distribution des nombres premiers >>> Anglais

FONCTION DE MÖBIUS (n)

FONCTION DE MERTENS M(n)

Une fonction curieuse liée aux facteurs d'un nombre, définie par Möbius en 1832, et une autre déduite de celle-ci.

Par le même Auguste Möbius (1790-1868) que celui du ruban

Voir Types de nombres selon leurs facteurs

FONCTION DE MÖBIUS
Définition La fonction (n) (mu de n) compte la nature des facteurs de n. Elle est construite de la manière suivante:

Si un des facteurs se répète	(n) = 0
12 = 1 x 2 x 2 x 3	(12) = 0
25 = 5 x 5	(25) = 0
Si le nombre est premier ou Si tous les facteurs sont distincts et si leur quantité est impaire et par définition si n = 0	(n) = – 1
2 est premier	(2) = –1
3 est premier	(3) = –1
70 = 2 x 5 x 7	(70) = –1
Si tous les facteurs sont distincts et si leur quantité est paire et par définition si n = 1	(n) = 1
6 = 2 x 3	(6) = 1

Formulation abrégée

(n) =		0	si n a au moins un facteur répété;
		1	si n = 1;
		(–1)^k	si n est le produit de k facteurs premiers distincts.

Voir Nombre sans facteur carré / Cousins des nombres premiers

Valeurs pour les premiers nombres

1	2	3	4	5	6	7	8	9	10
1	2	3	2x2	5	2x3	7	2x2x2	3x3	2²x5
Valeur de (n)
			0				0	0
1					1				1
	-1	-1		-1		-1

11	12	13	14	15	16	17	18	19	20
11	2^2x 3	13	2x7	3x5	2^4	17	2x3²	19	2²x5
Valeur de (n)
	0				0		0		0
			1	1
-1		-1				-1		-1

Suite >>>

FONCTION DE MERTENS

Définition

La fonction M (n) s'appuie sur celle de Möbius: il s'agit de la somme de toutes les valeurs de la fonction de Möbius jusqu'à n.

M(n) = somme de tous les (n)

à partir de n = 1.

Valeurs pour les premiers nombres

1	2	3	4	5	6	7	8	9	10
Valeur de M (n)
1	0	-1	-1	-2	-1	-2	-2	-2	-1

11	12	13	14	15	16	17	18	19	20
Valeur de M (n)
-2	-2	-3	-2	-1	-1	-2	-2	-3	-3

Suite >>>

Conjecture de Mertens (fausse)
La valeur absolue de M(n) est toujours inférieure à n, & Si l'on peut prouver que la valeur absolue de M(n) est toujours inférieure à n, alors l'hypothèse de Riemann est vraie.
Cette conjecture est passée pour vraie pendant longtemps. En 1984, Andrew Odlyzko et Hermante Riele montrent qu'il existe un nombre plus grand que 10^30 qui infirme la conjecture. La conjecture si elle avait été vraie aurait permis de conclure sur l'hypothèse de Riemann. La conjecture étant fausse elle ne permet pas de conclure sur l'hypothèse de Riemann. Mais ne l'infirme pas non plus. Remarque Cette découverte montre la modestie que doivent inspirer les conjectures: vraies jusqu'à des nombres incroyablement grands et qui déraillent dans les très hautes sphères.

UTILISATION

Il a été montré que la conjecture de Riemann est équivalente à la conjecture suivante:

M(n) ne croît pas plus vite que k . N^{1/2 + e}

avec e arbitraire, mais plus grand que 0.

Amusant! Encore un autre pont entre les nombres:

nombres premiers et ceux qui ont des diviseurs répétés.

La valeur de (n) est assez aléatoire. Cependant, quelle est la probabilité que n n'ait pas de facteurs répétés?

Il ne doit pas être multiple de 4, de 9, de 25… de p²
Soit pas carré d'un premier.

La probabilité que n ne soit pas un multiple de 4 est ¾
Pas un multiple de 9 est 8/9
Pas un multiple de 25 est 24/25
etc.
Ces conditions sont indépendantes.
Donc la probabilité que ne soit pas égal à 0 est (3/4) (8/9) (24/25) (48/49) …
Or ce produit tend vers 6 / ²

Conclusion :

Probabilité que  (x) =	-1	0	+1
est égale à:	3 / ²	1 – 6 / ²	3 / ²

Faisons un raisonnement particulier,

En prenant une grande quantité de nombres au hasard, les probabilités indiquées dans le tableau s’appliquent.
Ajoutons toutes ces probabilités pour tous les nombres choisis.
L’occurrence de +1 devrait être du même ordre que celle de –1.

En fait,

Il existe un théorème en probabilité (inégalité de Hausdorff) qui dit que :

Avec une grande quantité de nombres pris au hasard,

la somme ne croît pas plus vite que k.N^1/2+e

lorsque N tend vers l’infini,

et ceci avec une probabilité de 1.

C’est exactement la conclusion cherchée

Hélas,

Il y a une différence importante
Ici, on a pris des nombres au hasard,
alors qu’il faudrait avoir la même chose avec les nombres de 1 à N.

Good et Churchhouse ont fait de nombreux calculs
et trouvèrent une excellence confirmation expérimentale
de ce modèle en (n)

Entre 0 et 33 000 000, ils ont trouvé 12 938 407 valeurs pour lesquelles (x) = 0

Le calcul de probabilité donne 33 000 000 x (1 - 6/²) = 12 938 405,6

En physique,

Avec de tels résultats (8 décimales), on serait heureux et catégorique quant à la conclusion.

En mathématique,

Ça n’est pas suffisant.
Mais, la présomption est tout de même très forte !

Voir Valeurs et courbes de la fonction de Mertens

Distribution des nombres premiers
La fonction de Möbius est très utilisée en théorie des nombres. Par exemple Les deux formules suivantes sont équivalentes au théorème des nombres premiers:

English definition

The Möbius function of a number n is denoted by (n) and applies only to whole numbers. If n is a prime number, (n) is defined as – 1. If n is a composite number, there are three possibilities: · at least one of the prime is repeated, in which case (n) = 0; · or there is an even number of different primes, in which case m (n) = + 1; · or there is an odd number of different primes, in which case m (n) = – 1. To find the Mertens function M(n), you add up all the values of the Möbius function from 1 to n.

Retour	Identité d'Euler et hypothèse de Riemann
Suite	Tables de valeurs Möbius et Mertens Fonctions arithmétiques – Liste Lambda (n) et fonction de Liouville Conjecture des premiers jumeaux et fonction de Moebius
Voir	Calcul et calcul mental Divisibilité Euler – Index Géométrie – Index Identités remarquables Isopérimètre Kronecker et matrices Nombres premiers Petit théorème de Fermat  Ruban de Moebius Série Harmonique Théorie des nombres – Index
Site	Edmund Georg Hermann Landau
Livres	La symphonie des nombres premiers – Marcus du Sautoy – Points Sciences (Héloïse d'Ormesson) – 2005. Superbe! Livre de poche de 500 pages qui se lit comme un roman. Raconte toute cette recherche pour prouver la conjecture de Riemann tout en faisant quelques détours mathématiques intéressants. Appréciable aussi, l'atmosphère du monde des chercheurs en mathématiques. Karl Sabbagh – Dr. Riemann's zeros The search for the $ 1 million solution to the greatest problem in mathematics – Atlantic book London – 2003
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Identite/Mobius.htm