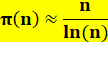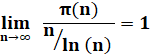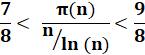|
Édition du: 01/02/2023 |
|
INDEX |
Nombres Premiers – Quantité |
||
NP: Nombres premiers
![]()
|
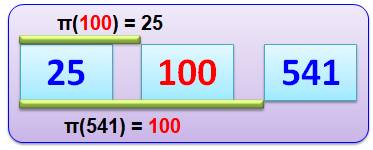
FONCTION Pi(n) QUANTITÉ de nombres
premiers jusqu'au nombre n compris. Elle est
caractérisée par la fonction nommée π(n) Exemple: Il y a 1 229 nombres premiers < 10
000. On écrit: π(10 000) = 1 229. |
||
|
|
Sommaire de cette page >>> Fonction >>> Bilan >>> Divisibilité de n par Pi |
Débutants Glossaire |
Curiosité unique
|
|
Seule
forme connue.
Voir Nombre 59 |
|
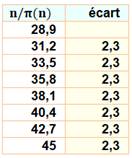
Définition La fonction
Dans
le tableau, le ratio de la colonne de droite augmente de 2,3 pour chaque
puissance de dix successive. Cette
valeur est en fait le log népérien de 10. Voir
Table |
Pour
les nombres de 1 à 10 (En rouge, les nombres premiers)
|
|
Ne pas confondre !
|
Pi(n) = Quantité
de nombre premiers inférieurs
à n. Phi(n) = Quantité de nombres premiers avec n et inférieurs à
n. |
|
|
Progression de |
||
|
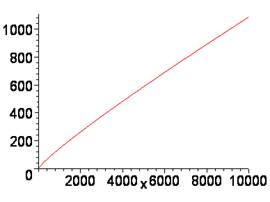
Courbe
de progression Traçons cette courbe n = f (ln(n))
En
construisant le graphe de |
Courbe
n / ln (n)
|
|
|
Théorème des nombres premiers Prime Number Theorem |
||
|
Théorème
des nombres premiers
Théorème de Tchebychev Tchebychev
Limits Theorem
|
En 1998, Pierre Dusart (université de Limoges) a montré que la
quantité de premiers inférieurs ou égaux à n est supérieure ou égale à cette expression
pour n supérieur à 6 000.
Autres formules d'approximation sur la page de Chris
Caldwell. |
|
|
Nombres
premiers autour de 10 000 000
|
La probabilité pour qu'un
nombre pris au hasard soit premier est environ 1 / log(n). Exemple log
10100 = 230
Un
nombre de 100 chiffres a
une chance sur 230 d'être premier |
|
|
On cherche les nombres multiples de
leur quantité de nombres premiers qui lui sont inférieurs |
Exemple
|
||
|
2 |
2, 4, 6, 8 |
||
|
3 |
27, 30, 33 |
||
|
4 |
96, 100, 120 |
||
|
5 |
330, 335, 340, 350, 355, 360 |
||
|
6 |
1008, 1080, 1092, 1116, 1122, 1128, 1134 |
||
|
7 |
3059, 3066, 3073, 3080, 3087, 3094 |
||
|
8 |
8408, 8424, 8440, 8456, 8464, 8472 |
||
|
9 |
23526, 23535, 24300 |
||
|
10 |
64540, 64580, 64610, 64620, 64650, 64690,
64700, 64710, 64720 |
||
|
11 |
175197 |
||
|
12 |
480852, 480864, 481008, 481020, 481032,
481044, 481056, 481068, 481080, 481092, 481296, 481356, 481368, 481404,
481416, 481428, 481440, 481452 |
||
![]()
|
Suite |
|
|
Voir |
|
|
Aussi |
|
|
|
|
|
Cette page |
![]()
Renvois
de liens suite à la refonte de ces pages
![]() DÉNOMBREMENT / Table Pi (n) >>>
DÉNOMBREMENT / Table Pi (n) >>>
![]() THÉORÈME DES NOMBRES PREMIERS >>>
THÉORÈME DES NOMBRES PREMIERS >>>
![]() Dénombrement & Table pi (n)
Dénombrement & Table pi (n)
![]() Le théorème des nombres premiers:
valeur de pi (n)
Le théorème des nombres premiers:
valeur de pi (n)
![]() Méthode de recherche des
nombres premiers
Méthode de recherche des
nombres premiers
![]() Analyse des unités et dizaines des premiers jusqu'à 1 000
Analyse des unités et dizaines des premiers jusqu'à 1 000
![]() Quantité de nombres premiers - Historique
Quantité de nombres premiers - Historique