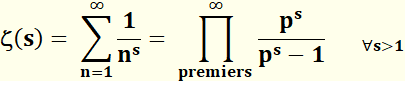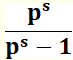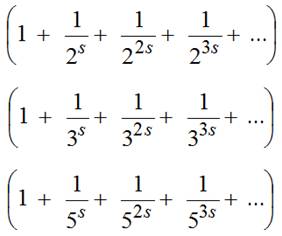|
||||||||||||||||||||||||||||||
![]()
|
IDENTITÉ d'EULER Démonstr Un peu coriace mais se laisse comprendre. Allons-y! Pas à pas. |
|
|
|
|
Formulation
Principe
de la démonstration
|
|
|
|
||||||||||||||||||
|
|
|
|||||||||||||||||
|
Voici les premiers facteurs |
|
|||||||||||||||||
|
Donnons
une forme générique à chacun des termes T de la somme monstrueuse. |
||||||||||||||||||
|
23 .33 = 8 . 27 |
T
= 2 a .
3 b .
5 c .
7 d … |
|||||||||||||||||
|
|
||||||||||||||||||
|
|
||
|
a 0 = 1 b
1 = b a
0 .
b1 = 1 . b = b |
a = 1, b = 1, c = 1, d = 1 … a = 2, b = 1, c = 1, d = 1 … … a = 5, b = 1, c = 1, d = 1 … … a = 2, b = 2, c = 1, d = 1 … … et même a = 1, b = 0, c = 0, d = 0 … a = 0, b = 1, c = 0, d = 0 … … |
|
|
|
T = { 20 , 21 , 31 , 51
, 21
. 31 , 22 . 31 , 21
. 32 . 51 , … |
|
|
|
Tout entier est le
produit unique de nombres premiers (facteurs) |
|
|
|
CQFD
|
|
|
|
|
|
|
|
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()