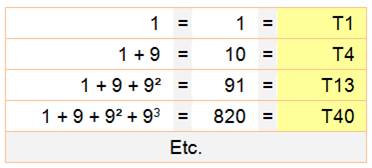|
||||||||||||||||||||||||||||||||||||||||
![]()
|
|
|
|
Voir
Fibonacci / Pyramidaux Somme des nombres
triangulaires:
Voir Table Somme des puissances de 9:
Nombres triangulaires et
carrés 1,
36, 1225, 41616, 1413721, 48024900... Voir Nombres
carrés Nombres triangulaires et
pentagonaux 1, 210, 40755, 7906276, 1533776805,
297544793910, ... Voir Nombres
pentagonaux |
|
Voir
Carrés / Cubes / Somme
de carrés / Somme de cubes
|
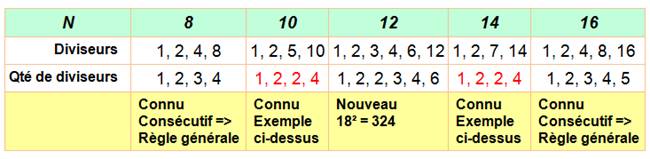
CARRÉS
& CUBES – Généralisation Méthode de Joseph Liouville
(1809
- 1882) |
|
|
|
Méthode |
Exemple |
|
|
|
6 |
|
|
|
1,
2, 3, 6 |
|
|
|
1, 2, 2, 4 |
|
|
|
13
+ 23 + 23 + 43 =
(1 + 2 + 2 + 4)2 =
81 |
|
|
Exemples
|
||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
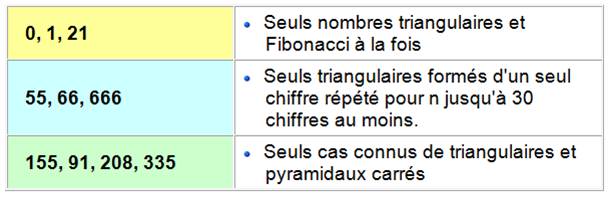
Couple de nombres triangulaires dont la somme et la
différence sont aussi des nombres triangulaires. Liste
des triangulaires jusqu'à 2000 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66, 78,
91, 105, 120, 136, 153, 171, 190, 210, 231,
253, 276, 300, 325,
351, 378, 406, 435, 465, 496, 528, 561, 595,
630, 666, 703, 741, 780,
820, 861, 903, 946, 990,
1035, 1081, 1128, 1176, 1225, 1275, 1326,
1378, 1431, 1485, 1540, 1596, 1653, 1711, 1770,
1830, 1891, 1953, 2016, >>> Premiers
membres de tels quadruplets 15, 105,
378, 780, 2145, 1485, 5460, 7875, 29403, 21945, 70125, 105570, 61425, 37950,
255255, 306153, 61425, 667590, 749700, 522753, 1016025, 353220, 176715,
1471470, 1445850, 1747515, 246753, 794430, 749700, 514605, 3499335, 2953665,
5073705, 635628, 8382465, … |
Quadruplets de nombres triangulaires
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Programme
Maple
|
Commentaire Procédure
de recherche si N est un nombre triangulaire. Recherche si la racine ce cette
équation est entière: N
= x (x + 1) / 2 2N
= x² + x La
procédure retourne la valeur de x et 0 si le nombre n'est pas triangulaire. Le
programme principal calcule une paire de triangulaires T1 et T2, leur somme
T3 et leu différence T4. Impression
du quadruplet si ces deux derniers nombres sont triangulaires. Résultat
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Voir Programmation – Index
![]()
|
Suite Nombres
triangles |
|
|
Voir Nombres géométriques |
|
|
Voir |
|
|
DicoNombre |
|
|
Site |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Geometri/NbTrianC.htm |
![]()