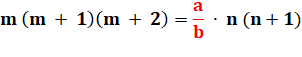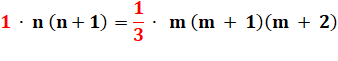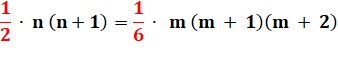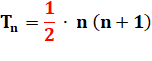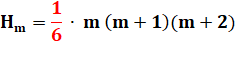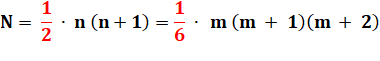|
|||||||||||||||||||||||||||||||||
![]()
|
NOMBRES CONSÉCUTIFS Produit de consécutifs = Produits
d'autres consécutifs Quels sont les produits de p consécutifs égaux au
produit de q consécutifs avec une pondération k. Ils sont très nombreux … Exemples avec k = 3 puis k = 2/3
Exemple: nombre triangulaire = nombre tétraédrique
(le plus grand)
|
|
|
||||
|
Reprenons
l'exemple sous forme générique. |
|
|||
|
Avec le
rapport k = 3, il a exactement cinq solutions. |
1 x 2 x 3 3 x 4 x 5 8 x 9 x 10 20 x 21 x 22 34 x 35 x 36 |
= 3 x 1 x 2 = 3 x 4 x 5 = 3 x 15 x16 = 3 x 55 x 56 = 3 x 119 x 120 |
= 6 = 60 = 720 = 9 240 = 42 840 |
|
|
Nouvelle
écriture ave k = a/b |
|
|||
|
Variantes
de l'écriture de l'équation
diophantienne avec (exemple): |
|
|||
|
|
||||
|
Les nombres
triangulaires sont de la forme indiquée. On sait que tout produit de deux
nombres consécutifs est divisible par 2. Les nombres
tétraédriques sont de la forme
indiquée. On sait que tout produit de trois nombres consécutifs est divisible
par 6. |
|
|||
|
D'où
l'intérêt de la dernière identité ci-dessus qui considère les nombres qui
sont à la fois triangulaires et tétraédriques. |
|
|||
|
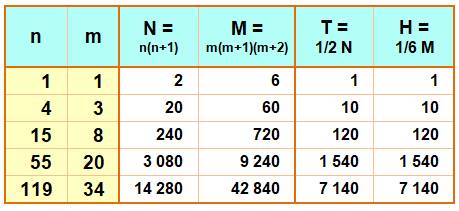
Les cinq
seuls tels nombres sont: |
|
|||
|
Ce sont
les seuls. |
Prouvé en 1966 par E.T. Avanesov. |
|||
Suite et programmation
en Nombres
tétraédriques
![]()
Liste de tels nombres
|
|
||
|
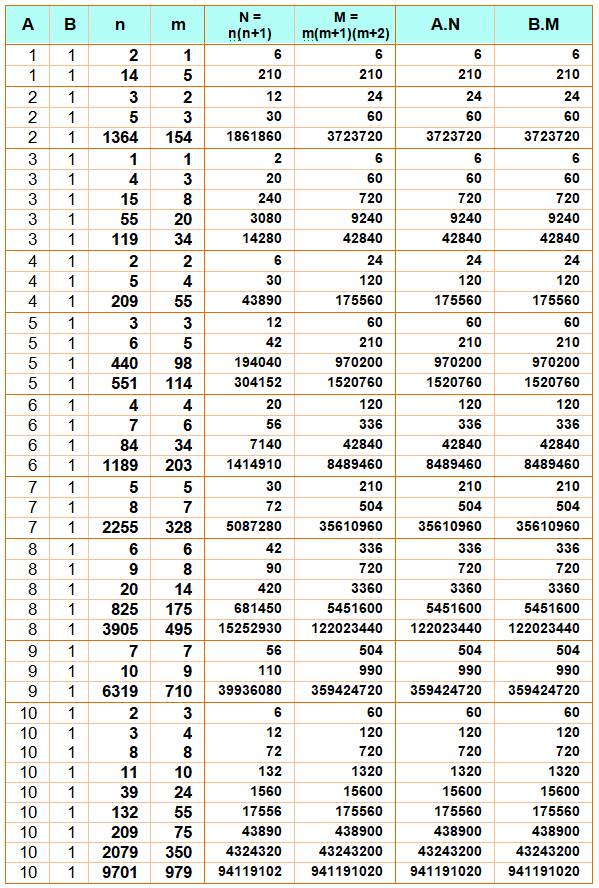
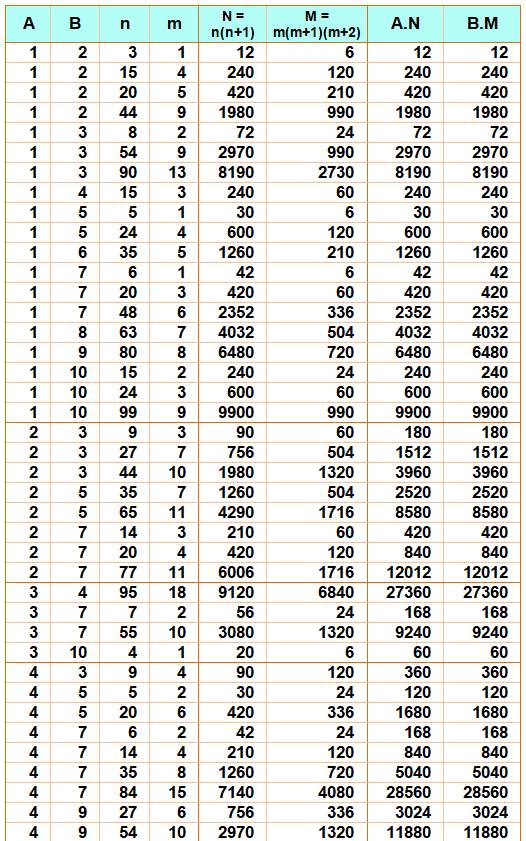
Exemple de lecture A = 2 et B = 1 n = 5 et m
= 3 Alors N = 5 x 6 = 30 M = 3 x 4 x 5 = 60 Ce qui conduit à: A.N = 2 x 30 = 60 B.M = 1 x 60 = 60 Les lignes A = 3 reproduisent les résultats
trouvés ci-dessus. |
Tableau
établi jusqu'à n = m = 10 000, A jusqu'à 10 et B = 1
|
|
|
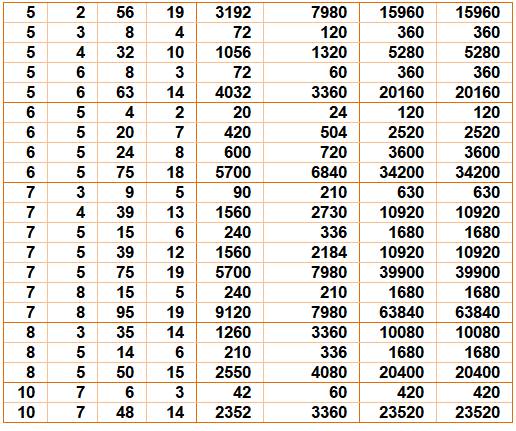
Exemple de lecture A = 2 et B = 3 n = 9 et m
= 3 Alors N = 9 x 10 = 90 M = 3 x 4 x 5 = 60 Ce qui conduit à: A.N = 2 x 90 = 180 B.M = 3 x 60 = 180 |
Tableau
établi jusqu'à n = m = 100, A
jusqu'à 10 et B = 2 à 10 et A et B premiers entre eux
|
|
|
||
|
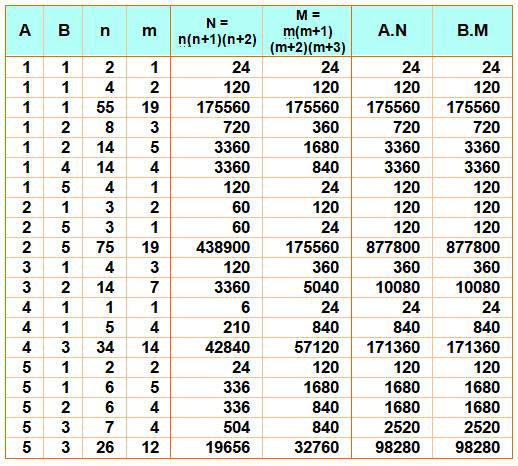
Exemple de lecture A = 2 et B = 5 n = 3 et m
= 1 Alors N = 3 x 4 x 5 = 60 M = 1 x 2 x 3 x 4 = 24 Ce qui conduit à: A.N = 2 x 60 = 120 B.M = 5 x 24 = 120 |
Tableau
établi jusqu'à n = m = 100, A jusqu'à
5 et B = 1 à 5 et A et B premiers entre eux
|
|
![]()
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Decompos/CONSECUT/ProdProd.htm
|
![]()