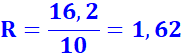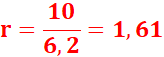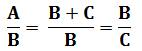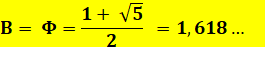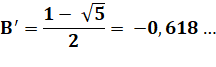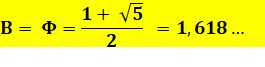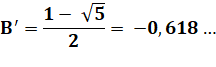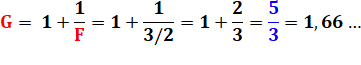|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
NOMBRE D'OR en bref Ce qui est essentiel à savoir Tour d'horizon en commençant par approcher le nombre d'or
par la construction du rectangle d'or et en finissant par un édifice, le
Parthénon, dont les dimensions sont sensées démontrer le nombre d'or. |
Notation

|
Nombre d'or ou divine proportion Inverse et carré: mêmes décimales
|
|
Voir Nombre 1,618… / Nombre
2,4142… / Nombre
3,1415… / Brève
527 / Constante
Pi / Nombre
d'argent
|
|
||||||||||||||||||||||||||||||||
|
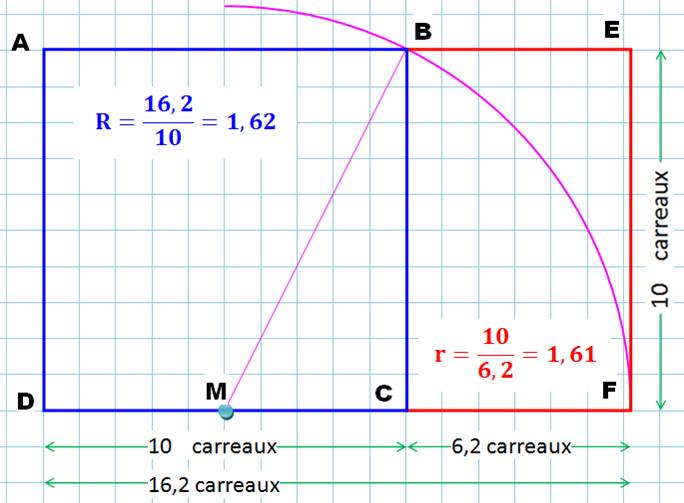
Étapes
de construction 1)
Je construis un carré ABCD
de 10 carreaux de côté. 2)
Je positionne le point milieu M, en bas. 3)
Je dessine un cercle de centre
M et de rayon MB; il coupe la droite DC en F. 4)
Le rectangle
ABEF est un rectangle d'or.
Mesures
et conclusions Je
mesure le grand côté DF: 16,2 carreaux Le
rapport (ou le quotient)
entre les mesures de la longueur et de la largueur est
Si
je calcule le rapport pour le rectangle BEFC, je trouve
Soit,
à peu près la même valeur. Ce
nouveau rectangle BEFC est aussi un rectangle d'or. Valeur
exacte du nombre d'or Le
triangle BCM est rectangle, je peux lui
appliquer le théorème de Pythagore:
Cette
valeur confirme les mesures effectuées sur les deux rectangles. |
||||||||||||||||||||||||||||||||
|
|
||
|
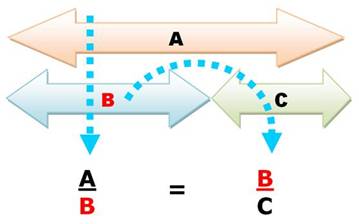
Le nombre d'or, aussi appelé divine proportion,
est justement défini par une proportion. Un segment est coupé en deux selon
la divine proportion si: "le
long est au moyen ce que le moyen est au petit". |
|
|
|
Cette proportion se prête à un
calcul. En se rappelant que A = B + C. |
|
|
|
En prenant la forme linéaire. |
B² = (B + C) x C = BC + C² |
|
|
Soit une équation du second degré. En choisissant C = 1. |
B² - BC – 1 = 0 |
|
|
Sa résolution donne deux valeurs
pour B. En fait, le nombre d'or (noté phi majuscule). |
|
|
Voir Résolution d'un équation étonnante
dont la racine est le nombre d'or
|
|
|||
|
En géométrie, nous avons construit le rectangle d'or.
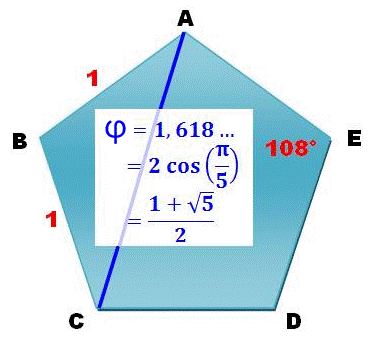
En fait, le nombre d'or est roi dans le pentagone où
il se niche quel que soit le pentagone pourvu qu'il soit régulier. La longueur de la diagonale d'un
pentagone régulier de côté unité est égale au nombre d'or. C'est le cas pour les cinq
diagonales: AC, AD, BE, BD et CE. Note: si vous calculer la valeur du cosinus avec votre calculette, assurez-vous que
vous êtes bien en position: radians
(Pi/5 radian = 36°).. |
|
||
|
En arithmétique, le nombre d'or est
le nombre vers lequel converge le rapport entre deux nombres successifs de la
suite de Fibonacci. Cette suite de nombres est
rencontrée couramment dans la structure des végétaux (phyllotaxie) |
Suite de Fibonacci: 1, 1, 2, 3, 5, 8, 13, 21 … Chaque nombre est la somme des deux précédents. Déjà avec 21/13 on trouve: 1,615 Avec de plus grands nombres comme 233/144, on trouve:
1,6180 … C'est
d'ailleurs une bonne approximation de Phi, facile à retenir. |
||
|
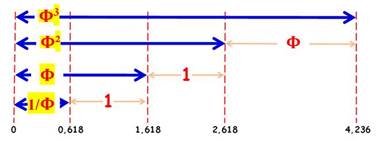
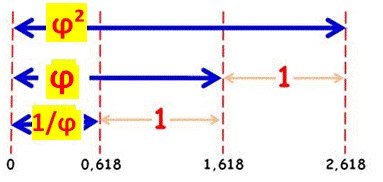
Curiosité avec les puissances Le nombre d'or au carré conserve ses décimales. C'est le cas également pour
l'inverse du nombre d'or. 0,618 … / 1,618… / 2,618… |
|
||
|
Curiosité avec les fractions Le nombre d'or est égal à une
fraction à étage qui se prolongerait sans fin. Ces drôles de fractions (fractions
continues) reproduisent les nombres de Fibonacci au numérateur et au
dénominateur. |
Etc. |
||
|
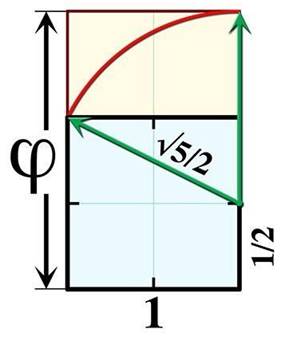
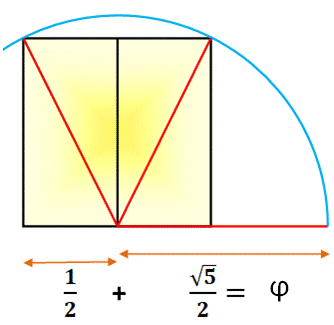
Construction géométrique La diagonale du rectangle (2, 1)
mesure racine de 5 (Pythagore). Elle est prolongée d'une unité à
l'aide d'un arc de cercle: segment rouge. Puis divisé par 2. Le segment bleu
mesure exactement Phi. |
|
||
|
Dans la vie courante: le format de la carte
de crédit est un rectangle d'or. Par contre, le format du papier A4 est dans un rapport racine de 2 =
1,414… >>>
|
|
||
|
Architecture moderne: Le Corbusier (1887-1965) est un architecte
qui à développé toute une théorie autour de l'harmonie du nombre d'or Il invente le Modulor qui sera son
abaque pour la construction des habitations. >>> |
|
||
|
En botanique Que ce soit au niveau des fleurs ou de la disposition des feuilles
ou des graines (comme celles du tournesol) on retrouve la suite de Fibonacci
et donc le nombre d'or. |
|
||
|
Conclusion |
S'il est vrai que ce nombre, associé
à la suite de Fibonacci, prend une place remarquable dans note univers, il ne
faut pas trop lui en demander. Nombreux sont ceux qui ont voulu
voir le nombre d'or un peu partout, au prix de considérations parfois
oiseuses. |
||
|
Parmi
tous les formats rectangulaires de la vie courante, rares sont ceux qui utilisent
le nombre d'or, pas même le format des toiles à peindre.
|
Voir Format
télévision / Format A3-A4 … / Appareils multimédia
|
|
||
|
Malgré les proportions imaginées sur
le Parthénon et d'autres édifices de l'Antiquité, il
n'existe aucune preuve que le nombre d'or fut connu à cette époque. |
Seul Euclide (325 – 265 Il faut attendre 1445 pour que Luca
di Borgo reprenne cette proportion et la "divinise". Le titre de
son livre: De divina proportione.
|
|
|
Fibonacci
(1175-1250) découvre la suite de nombres qui portera son nom et observe le
rapport. Plus les nombres sont grands et plus le rapport se rapproche de la
divine proportion, le nombre d'or. |
Léonard de Vinci (1452-1519)
réfléchit aux proportions idéales du corps humain,
basées sur le nombre d'or qu'il désigne par " sectio aurea " |
|
|
Commence alors un engouement pour ce
nombre.
|
||
|
C'est Ghyka, un prince roumain, qui
donnera le nom de nombre d'or. Lui aussi, tente de prouver le pouvoir
esthétique de ce nombre |
Le
Corbusier (1946) découvre dans le nombre d'or le secret d'une
construction en série en inventant le Modulor, système de proportions
architecturales pour une harmonie et une plus grande rapidité de
construction. |
|
Voir Historique
complet
|
|
||
|
Cet édifice est souvent cité* comme exemple de la connaissance du
nombre d'or chez les Grecs Anciens. L'édifice Temple, dédié à la déesse Athéna,
situé sur l'Acropole d'Athènes en Grèce. Il a été construit il y a environ 2
500 ans, du temps où Périclès a entrepris la reconstruction d'Athènes en
ruine après une attaque des Perses. Il abritait une statue géante
d'Athéna qui fut détruite lors d'une explosion en 1687. En effet, le temple a
servi d'église, puis de mosquée, et même comme dépôt de munitions par les
Turcs en guerre avec l'Italie. Lors des tirs italiens, la poudre en réserve
explose et détruit une grande partie du Parthénon. |
|
|
|
Parthénon
et rectangles d'or
|
||
Voir Parthénon
/ Géographie
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Geometri/NbOrBref.htm
|
![]()