NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 24/02/2015 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique
	Topologie
Débutants Géométrie	Dimensions			Glossaire Géométrie
INDEX Topologie Géométrie	Repères	Degrés de liberté	Dimensions 3D	Dimension 4D
		Sommaire de cette page >>> Les trois dimensions de l'espace >>> La 3D et la vie

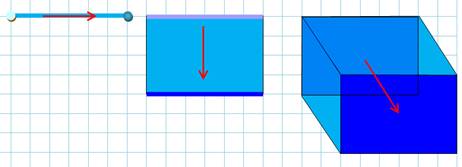
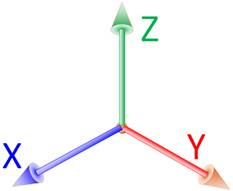
Dimensions – 3D

Troisième dimension. Notre monde géométrique classique.

Les trois dimensions de l'espace
Les trois dimensions nous sont familières en géométrie: D1: une ligne est engendrée par le déplacement (translation) d'un point; D2: une surface est engendrée par la translation d'un segment; et D3: un volume est engendré par la translation d'une surface.
Pour caractériser un point dans un espace à n dimensions, il faut donner n nombres. D1: un nombre sur X, l'abscisse; D2: deux nombres; un en plus sur Y, l'ordonnée; et D3: trois nombres; encore un en plus sur Z, la cote.

3D et la vie

La troisième dimension de l’espace est indispensable pour la vie. Imaginons un monde à 2D (Platpays ou Flatland): Alors, l’épaisseur n’existe pas! Un animal dans un monde 2D ne pourrait pas disposer d’appareil digestif: un tube qui relie les deux ouvertures sépare le corps en deux parties indépendantes. Ou, alors, il faudrait une autre anatomie qu'on ne peut pas imaginer Si la 3D est la marque de la vie humaine et animale, que penser de la 4D ? Les génies, les surhommes, les dieux ? Notez que construire une maison dans un monde à deux dimensions est certes possible; mais pas les portes ou les fenêtres. La maison s'écroulerait. Sauf à imaginer une gravité différente de la nôtre.

Suite	Degrés de liberté Dimension fractale
Voir	Quatre couleurs Topologie – Index Couleurs Ensemble
Livre	Flatland (1884) – Edwin Abbott Abbott – E-book gratuit
DicoNombre	Nombre 2 Nombre 3
Cette page	http://villemin.gerard.free.fr/aMaths/Topologi/Dimensio.htm