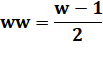|
||||||||||||||||||||||||||||||||
![]()
|
Mathématiques des Carrés Magiques Programmation de la méthode "TAPIS" Rappel de
la méthode et explication de l'algorithme de programmation. |
|
|
|||||||||||||||
|
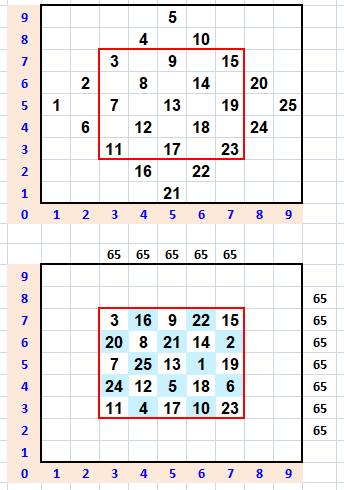
Cette
méthode est sans doute la plus simple à réaliser, mais elle ne s'applique
qu'aux carrés d'ordre impairs. Exemple de construction avec le 5x5 Elle consiste à disposer les nombres croissants
le long de diagonales dans un carré 9x9 pour construire le carré 5x5 (en
rouge) La seconde étape consiste à translater les
triangles qui dépassent jusqu'u fond du carré rouge. |
|
||||||||||||||
|
Quelques notations |
|
||||||||||||||
|
|
|||
|
Grand carré Le principe consiste à créer la matrice A pour y
inscrire les nombres selon la disposition en losange. Le positionnement de chaque nombre n progresse de
5 puis revient en arrière d'un cran pour re-progresser de 5. Ce cycle de 5 fait penser à un calcul avec modulo (reste
de la division par 5). Le déplacement d'un cran fait penser au quotient
de la division par 5. |
|
||
|
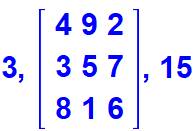
Carrés central Extraction des nombres du centre qui constituent
le cœur du carré magique. La suite va consister à combler les places vides
(du moins à "0"). |
|
||
|
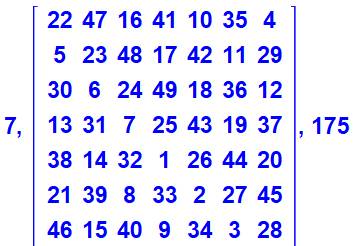
Carrés latéraux Extraction des nombres qui dépassent et placement
dans une matrice identique à la matrice finale |
|
||
|
Carré magique final On fait tout simplement l'addition des cinq
matrices, les quatre matrices latérales remplaçant justement les
"0" par les nombres adéquates. |
|
||
|
|
||||
|
|
Commentaires Appel des logiciels de manipulation des matrices
(Array). Calcul des paramètres w et ww. Demande de présentation de la table (interface), nécessaire pour les matrices de plus
de 10x10. Avec Matrix,
on forme la matrice du grand carré remplie de "0". La boucle énumère les nombres à placer dans la
matrice A en losange. Pour cela on calcule la valeur des coordonnées x et y
où l'on placera le nombre n. Ces coordonnées boucles (mod
w) sur la taille du carré et progresse d'un cran (iquo
= quotient) à chaque fois. Notez que le modulo impose de commencer avec n =
0, c'est pourquoi les coordonnées et le nombre sont incrémentés de 1 pour
forme la matrice A. |
|||
|
|
On va maintenant former les cinq matrices:
centrale (M), haut (H), gauche (L pour left), droite (R pour right, le D
étant réservé en Maple) et bas (B). Noter l'usage d'un mapping avec la flèche qui indique que chacun des i, j va
prendre une valeur. sous la condition
(if) Pour H,
nous obtenons les valeurs en haut de la matrice, il faut les
translater vers le bas avec la boucle
en k Pour L, il faut désigner une colonne. On indique
que tous les i sont à prendre pour la valeur j. Les cinq matrices sont additionnées pour former
le carré magique CM. |
|||
|
|
On vérifie que le carré est bien magique. Les sommes en colonnes sont calculées avec AddlongDimension et le paramètre 1; Conversion en
un ensemble qui élimine des doublons. Ici, on aura {175} et non [175,175,
175, 175, 175]. Même chose en lignes avec le paramètre 2. Les diagonales sont calculées en additionnant
toutes les cellules avec mêmes indices i et j pour l'une et opposés pour l'autre. Si toutes ces sommes sont égales, on imprime le
carré avec l'ordre et la somme magique. |
|||
|
Listing pour copier-coller dans
Maple |
with(ArrayTools):
w := 5: ww := (w-1)*(1/2): interface(rtablesize = 2*w): A := Matrix(2*w-1): for
n from 0 to w^2-1 do x := (`mod`(n, w))+iquo(n, w): y := (`mod`(n,
w))+2*ww-iquo(n, w): A[x+1, y+1] := n+1 end do: A; M := Matrix(w, w, proc (i,
j) options operator, arrow: A[i+ww, j+ww] end proc): H := Matrix(w, w, proc
(i, j) options operator, arrow: `if`(i < ww+1, A[i, j+ww], 0) end proc):
for k to ww do H[k+ww+1] := H[k]: H[k] := H[ww+1] end do: L := Matrix(w, w,
proc (i, j) options operator, arrow: `if`(j < ww+1, A[i+ww, j], 0) end
proc): for k to ww do L[1 .. w, k+ww+1] := L[1 .. w, k]: L[1 .. w, k] := L[1
.. w, ww+1] end do: R := Matrix(w, w, proc (i, j) options operator, arrow:
`if`(ww+1 < j, A[i+ww, j+2*ww], 0) end proc): for k to ww do R[1 .. w, k]
:= R[1 .. w, k+ww+1]; R[1 .. w, k+ww+1] := R[1 .. w, ww+1] end do: B :=
Matrix(w, w, proc (i, j) options operator, arrow; `if`(ww+1 < i, A[i+2*ww,
j+ww], 0) end proc): for k to ww do B[k] := B[k+ww+1]; B[k+ww+1] := B[ww+1]
end do: M; H, B, L, R; CM := M+H+L+R+B; SC := convert(AddAlongDimension(CM,
1), set): SL := convert(AddAlongDimension(CM, 2), set): SD1 := add(CM[i, i],
i = 1 .. w): SD2 := add(CM[w+1-i, i], i = 1 .. w): if op(SC) = op(SL) and
op(SC) = SD1 and op(SC) = SD2 then print(w, CM, SD1) end if: |
|||
Voir Programmation – Index
Florilège








![]()
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/CarreMag/aaaMaths/Tapis.htm |
![]()