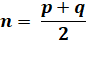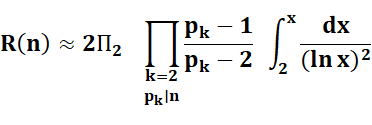|
Édition du: 27/10/2024 |
|
INDEX |
Partitions – Goldbach |
|||
![]()
|
Conjecture de GOLDBACH |
||
|
Terminale |
Sommaire de cette page >>> Conjectures forte et faible >>> Conjecture de la mi-distance >>> Historique >>> Vision résumée en 2014 >>> Témoignages de Schinzel et Sierpinski >>> Évaluation de la quantité de partitions >>> Goldbach et totient d'Euler >>> Bilan |
Débutants Glossaire |
|
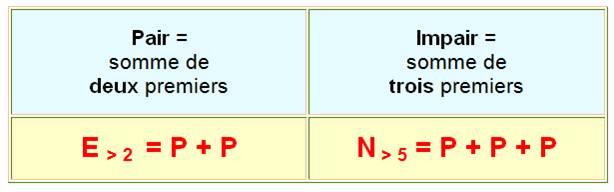
Formulations & historique de la CONJECTURE de GOLDBACH Il est curieux de voir
autant de mathématiciens cherchant à prouver des formules se rapprochant de celle
de Goldbach. Goldbach:
Les nombres premiers peuvent être répétés comme
dans 4 = 2 + 2 Notez cette propriété À
partir de 40, tous les nombres pairs sont
somme de deux nombres impairs composés. Voir Démonstration |
Voir Nombres premiers
Christian Goldbach (1690-1764 / 74 ans)
|
Mathématicien allemand (prusse); études à Königsberg. Il a vécu
principalement à Saint-Pétersbourg et à Moscou. Enseigne à Saint-Pétersbourg et y occupe des charges Correspond avec Leibniz,
Euler, Bernoulli. Ami avec Euler. Connu principalement pour sa conjecture: il semble au moins que tout nombre entier
plus grand que 2 est somme de trois nombres premiers (en ce temps, le nombre 1 était considéré
comme premier). |
Note: Gold Bach
veut dire ruisseau d'or en allemand
(das Gold und der Bach)
|
|
|||
|
Conjecture de Goldbach énoncée par Goldbach dans une lettre le 7 juin 1724, publiée en 1843. |
|
N = P + P + P |
|
|
Euler lui répond le 30 juin le problème est
difficile et peu se formuler ainsi: |
|
E = P + P |
|
|
Conjecture de Goldbach faible ou ternaire (Ternary Gloldbach Conjecture – TGC) |
|
O O: pour
nombre impair (odd en anglais) |
|
|
Autre conjecture de Goldbach |
En
fait, il existe une quantité finie d’exceptions. |
O = P +
2k² |
|
|
On
a montré que si
la conjecture de Goldbach faible est fausse, Elle ne l'est que pour un nombre fini de
cas. |
|||
|
Conjecture de Goldbach forte ou binaire (Binary Gloldbach Conjecture – BGC) |
|
E E: pour
nombre pair (even en
anglais) |
|
|
Si
la conjecture forte est démontrée, la faible l'est aussi. >>> Par
contre, la faible qui semble être démontrée en 2013, n'implique
pas que la forte le soit. |
|||
|
Variante de Schnizel (1930) |
|
N >
17 = P1 + P2 + P3 |
|
|
Variante équivalente
à BGC |
|
n + m = P n – m = P' 2n = P + P' |
|
|
Conjecture de Levy Il a formulé une conjecture un peu plus
forte |
|
O Vérifiée jusqu'à O
= 109 |
|
|
Conjecture de Lagrange (1775) Il avait conçu cette conjecture bien avant Levy! |
A conjecture of Lagrange asserts that
every odd integer greater than 5 can be written as a sum p + 2q, where both p
and q are primes. |
O >5
= P + 2.P |
|
|
Conjecture de Polignac Fausse |
|
O = P + 2k Non pour 127, 149 … |
|
|
Conjecture
cousine avec nombres composés |
|
E >12
= C + C |
|
|
Théorème de Chen |
|
E = P +
P.P E > 12 |
|
Explication sur la
variante en plus et moins m
|
Exemple Avec
20 = 2 x 10 = 3 + 17, le
nombre m est égal à 7, car P = 10 + 7 = 17 et P' = 10 – 7 = 3 Preuve Soit
un nombre pair somme de deux premiers: 2n = p + q. p
= 2n – q = n – (q – n) = n - m q
= = n + (q – n) = n + m |
Explication sur la cousine
|
Exemples 12
= 4 + 8; 13 = 4 + 9; 14 = 4 + 10; 15 = 6 + 9; 16 = 4 + 12 … Preuve Un
nombre pair peut s'écrire 10k, 10k + 2, 10k + 4; 10k + 6; 10k + 8 Or 10k = 15 + (10k – 15), somme de deux
composés; 10k
+ 2 = 15 + (10k – 8), somme de deux
composés; etc. Contre exemples pour n
impair 1
à 9, 11. Ce qui laisse penser que ce théorème est vrai pour tous les autres
nombres. |
|
Propriété Une conséquence directe de la conjecture forte |
Tout nombre n > 3 est à égale distance d'un couple de nombres
premiers, au moins une fois. ou: Tout nombre n > 1 est toujours représentable comme la demi somme
de deux nombres premiers. Every integer n > 3 is
halfway between two primes. |
|||||
|
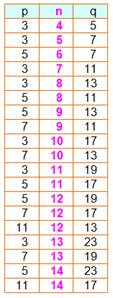
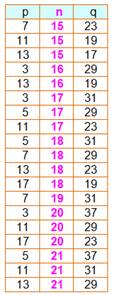
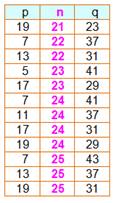
Exemple Le nombre 10 est à égale distance des nombres
premiers 3 et 17 ou encore de 7 et 13. Ce tableau montre que toutes les valeurs de n à
partir de 4 sont représentées. |
|
|||||
|
Conjecture de Goldbach Un nombre pair est la somme de deux premiers. Notez que n est alors la moyenne arithmétique des
deux premiers. |
2n = p + q n + n = p + q |
|
||||
|
Reformulation Cette relation montre que pour n quelconque, il existe
une paire de premiers tels que n est à égale distance de chacun (si la
conjecture de Goldbach est vérifiée !) |
n – p = q –
n |
|||||
|
Exemple avec 14 |
14 = 3 + 11 7 + 7 = 3 + 11 7 – 3 = 11 – 7 4 = 4 |
|||||
Voir Brève
49-964
Merci à Vittorio Ornago pour m'avoir
indiqué cette propriété surprenante
![]()
Conjecture de Goldbach: résumé de la situation en 2014
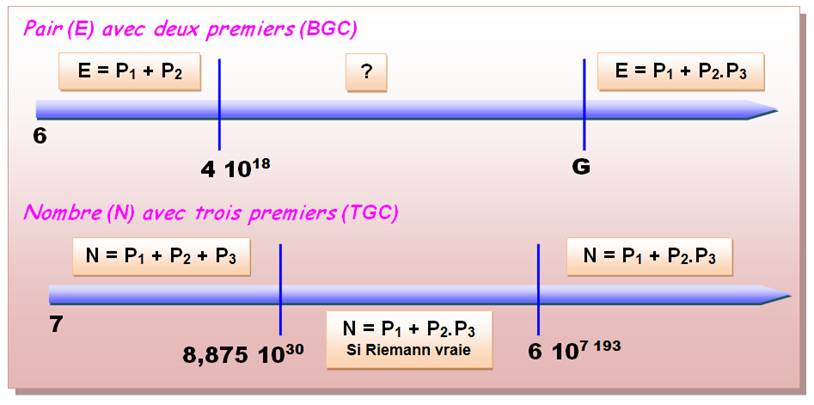
Sachant
que depuis 2013, la TGC (conjecture faible) serait démontrée.
D'après Number Theory for Computing – Song Y.
Yan – Page 297 + Mises à jour des valeurs
|
(Les nombres
mentionnés sont tous entiers et positifs) |
|
||
|
7 juin 1742 Goldbach |
|
N = P + P
+ P |
|
|
Euler répond à Goldbach |
Tout nombre pair supérieur à 2 est la somme
de deux premiers. |
E = P + P |
|
|
1770 Edward Waring |
|
||
|
1808 Adrien-Marie Legendre |
|
||
|
1843 |
|
||
|
1855 A. Desboves explore les |
|
104 |
|
|
1914 Harald Bohr Edmund Landau |
|
||
|
1920 Viggo Brun |
|
E = A + B A = P.P…P B = P.P…P 9 fois max |
|
![]()
|
1923 Hardy
& Littlewood |
|
O si Riemann |
|
1924 Hans Radmacher |
|
E = A + B A = P.P…P B = P.P…P 7 fois max |
|
1933 Lev Schnirelmann prouve
que: |
|
N = P + P
+ …+ P K fois max |
|
1937 Vinogradov prouve
que |
Hardy et Littlewood avaient démontré
la même chose mais supposant l'hypothèse de Riemann généralisée |
O corollaire E |
|
1938 Corpust Estermann Chdukov prouvent
que |
|
Il y en a moins de
|
|
1939 Schnirelmann prouve
que: |
|
E = P1
+ P2 + … + P300 000 |
|
1940 Pipping |
|
105 |
|
1947 Alfred Renyi prouve |
|
E > K = P + P.P…P K fois max |
![]()
|
1951 Yuri Linnik |
|
E >
K = P + P + 2a + 2b + … K fois max |
|
1956 Borodzkin |
|
n > 33^15
= 314348907 |
|
1959 Andrzej Schnizel prouve |
|
N = P1
+ P2 + P3 |
|
1964 Shen |
|
3,3 107 |
|
1965 Stein & Stein |
|
108 |
|
1966
(publié 1973) Chen Jingrun (1933-1996) |
|
E ou P + P . P Démontré G' > 12 |
|
1969 Klimov |
|
K = 115 elle est actuellement à 19 |
|
1975 Hugh Montgomery Robert Charles Vaughan |
|
E = P + P presque
toujours |
|
1977 Pogorzelski |
|
|
|
1989 Chen Wang |
|
n > 1043 000 |
|
1989 Granville, Lune, Riele |
|
2 1010 |
|
1989 Deshouillers, Riele, Saouter |
|
1014 |
|
1993 Sinisalo vérifie que |
|
4 x 1011 |
|
1989 Chen et Wang arrive à |
|
G |
|
1994 Vinogradov |
|
O G |
|
1995 Olivier Ramaré (Français) prouve |
|
E = P + P
+ …+ P 6 fois max corollaire N = P + P
+ …+ P 7 fois max |
|
1995 Kaniecki prouve |
|
si Riemann: E = P + P + …+ P 4 fois max O = P + P
+ …+ P 5 fois max |
|
1995 Saouter |
|
1020 |
|
1989 Deshouillers, Riele, Effinger, Zinoviev |
|
si Riemann
généralisé: E = P + P
+ P |
|
1998 Jörg Richstein |
|
4 1014 |
![]()
|
2002 Roger Heath-Brown J.-C. Schlage-Puchta |
|
K = 13 |
|
2003 Janos Pintz Imre Ruzsa |
|
K = 8 |
|
2003 Tomas Oliveira e Silva |
|
6 x 1016 |
|
2012 Tomas Oliveira e Silva |
|
4 x 1018 |
|
2012 |
|
O = P + P
+ P + P + P |
|
D. Platt |
|
8,8 1030 |
|
2013 Harald Helfgott |
|
G < 1027 |
|
2013 Harald Helfgott |
(preuve
en cours de vérif.) |
O = P + P
+ P |
Voir Explications
techniques sur histoire récente / Actualités
Extrait de Selecta
d'Andrzej Schinzel – Article écrit avec Sierpinski – Page 1114
|
|
|
|
Si
R(n) est la quantité
de partitions possibles d'un nombre pair en somme de deux nombres premiers,
la conjecture généralisée dit que:
où En
1923, Hardy et Littlewood conjecturèrent une formule de ce type. |
|
|
|
|
|
Si
la conjecture de Goldbach est vraie, alors pour tout nombre N, il existe deux
nombres premiers p et q tels que:
où En
se souvenant que, pour un nombre premier:
|
|
|
La
conjecture de Goldbach concernant la partition des entiers en nombres
premiers s'inscrit dans les listes des problèmes non résolus à ce jour. Notamment
dans la liste des 23 problèmes
établie par Hilbert (1900). Le 8e s'applique aux
nombres premiers; de même que l'un des sept
problèmes de la fondation Clay (2000) |
![]()
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
![]()