|
|||||||||||||||||||||||||||||||||||||||
![]()
|
CONJECTURE DE GOLDBACH Représentations graphiques Les trois méthodes
classiques de représentations de données relatives à la conjecture de
Goldbach. |
|
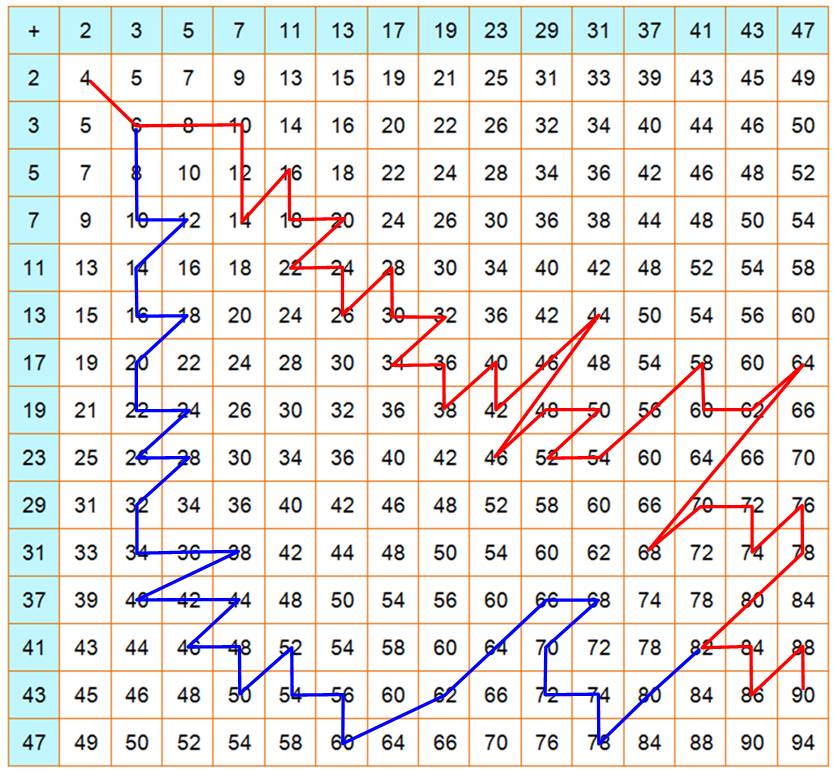
et deux chemins montrant tous les nombres pairs de 4 à 90 |
|
|
Table
d'addition classique à deux entrées, à la différence que les nombres entiers sont limités aux nombres premiers. Notez que la table est symétrique par rapport à
sa diagonale descendante. Mises à part la première ligne et la première
colonne impliquant le nombre 2, toutes les autres cellules sont paires.
|
|
Voir Exploitation
de cette table comme début de preuve
|
|
|
|
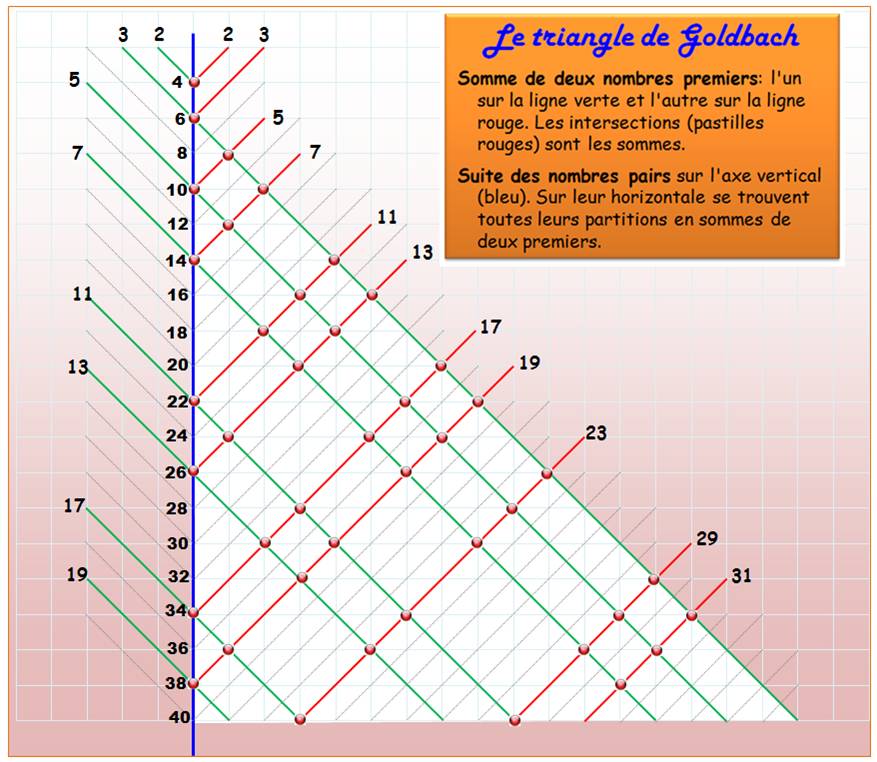
En reprenant la table d'additions, tournée de 45°, il
est possible de mieux visualiser toutes les partitions d'un coup d'œil pour
chaque nombre pair de la colonne centrale. Exemples
de lecture: 16
= 5 + 11 = 3 + 13; 18 = 7 + 11 = 5 +
13; …
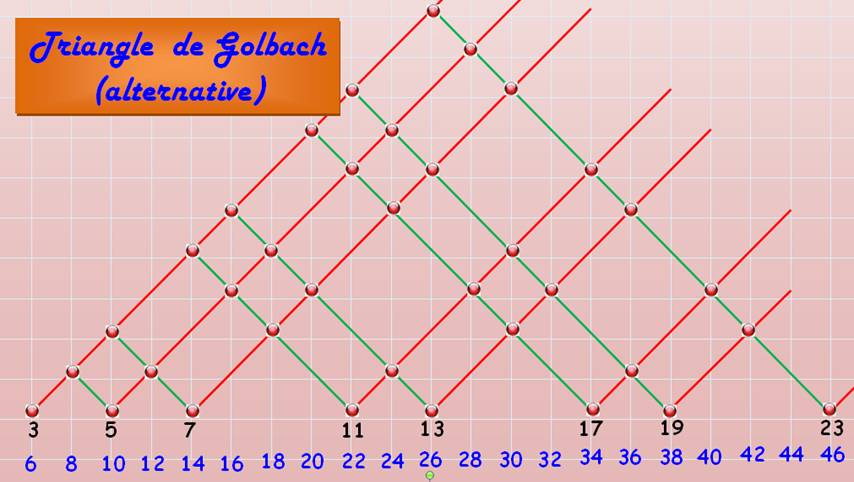
Une alternative graphique consiste à poser le triangle
isocèle sur sa base. Cette disposition montre sans doute mieux l'infinité des possibilités
offertes par chaque nombre premier. En effet le graphe se prolonge
indéfiniment vers la droite.
|
|
Voir Triangles
|
|
|
|
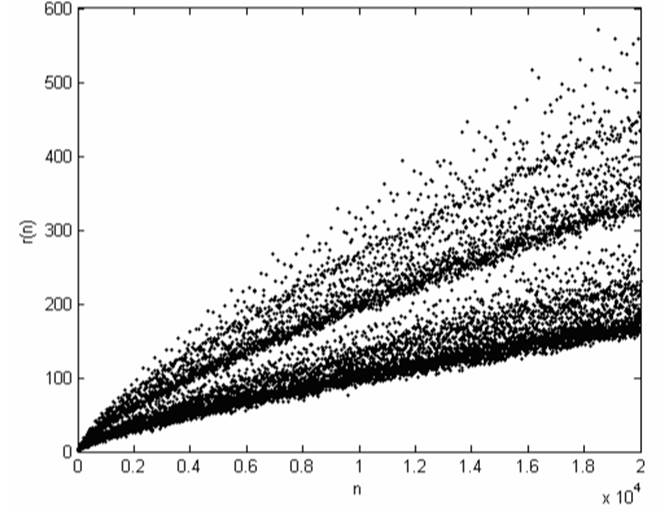
Il s'agit de représenter la quantité de partitions r(n) des nombres pairs
successifs (n).
Notez bien que le 1
en abscisse représente 10 000 = 104. Cette configuration, présentant deux bandes distinctes
et, surtout, avec son allure asymptotique, pourrait-elle se prêter à des
calculs de prédiction et finalement permettre la résolution
la conjecture? Voir Autre représentation en Preuve par probabilités |
|
Figure extraite de Fractal in the
statistics of Goldbach partition – Wang Liang, Huang Yan et Dai Zhi-cheng
![]()
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
![]()