NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 25/04/2020 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	PARTITIONS
Débutants Général	Conjecture de GOLDBACH				Glossaire Général
INDEX Partitions Général	Introduction	Représentation	Formulations	Preuve?
		Polignac	Historique	Tables Goldbach
		Sommaire de cette page >>> Nombres somme de deux premiers (1 à 100) >>> Nombres jamais somme de deux premiers >>> Records de quantités de partitions en deux premiers >>> Nombres somme de trois premiers (1 à 50) >>> Records de quantités de partitions en trois premiers

CONJECTURE DE GOLDBACH

Table de sommes de premiers

Nombres somme de deux nombres premiers ou de trois nombres premiers. Records de quantité de partitions.

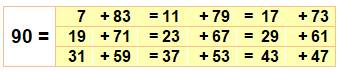
Le nombre 90 est neuf fois la somme de deux nombres premiers.

Nombres somme de deux premiers (1 à 100)

n = p1 + p2 = q1 + q2 + …

En jaune, record de multi-partitions.

n	p1	p2	q1	q2	r1	r2
4	2	2
5	2	3
6	3	3
7	2	5
8	3	5
9	2	7
10	3	7	5	5
12	5	7
13	2	11
14	3	11	7	7
15	2	13
16	3	13	5	11
18	5	13	7	11
19	2	17
20	3	17	7	13
21	2	19
22	3	19	5	17	11	11
24	5	19	7	17	11	13
25	2	23
26	3	23	7	19	13	13
28	5	23	11	17
30	7	23	11	19	13	17
31	2	29
32	3	29	13	19
33	2	31
34	3	31	5	29	11	23
34	17	17
36	5	31	7	29	13	23
36	17	19
38	7	31	19	19
39	2	37
40	3	37	11	29	17	23
42	5	37	11	31	13	29
42	19	23
43	2	41	3	41	7	37
44	13	31
45	2	43
46	3	43	5	41	17	29
46	23	23
48	5	43	7	41	11	37
48	17	31	19	29
49	2	47
50	3	47	7	43	13	37
50	19	31
52	5	47	11	41	23	29
54	7	47	11	43	13	41
54	17	37	23	31
55	2	53
56	3	53	13	43	19	37
58	5	53	11	47	17	41
58	29	29

60	7	53	13	47	17	43
60	19	41	23	37	29	31
61	2	59
62	3	59	19	43	31	31
63	2	61
64	3	61	5	59	11	53
64	17	47	23	41
66	5	61	7	59	13	53
66	19	47	23	43	29	37
68	7	61	31	37
69	2	67
70	3	67	11	59	17	53
70	23	47	29	41
72	5	67	11	61	13	59
72	19	53	29	43	31	41
73	2	71
74	3	71	7	67	13	61
74	31	43	37	37
75	2	73
76	3	73	5	71	17	59
76	23	53	29	47
78	5	73	7	71	11	67
78	17	61	19	59	31	47
78	37	41
80	7	73	13	67	19	61
80	37	43
81	2	79
82	3	79	11	71	23	59
82	29	53	41	41
84	5	79	11	73	13	71
84	17	67	23	61	31	53
84	37	47	41	43
85	2	83	3	83	7	79
86	13	73	19	67	43	43
88	5	83	17	71	29	59
88	41	47
90	7	83	11	79	17	73
90	19	71	23	67	29	61
90	31	59	37	53	43	47
91	2	89
92	3	89	13	79	19	73
92	31	61
94	5	89	11	83	23	71
94	41	53	47	47
96	7	89	13	83	17	79
96	23	73	29	67	37	59
96	43	53
98	19	79	31	67	37	61
99	2	97
100	3	97	11	89	17	83
100	29	71	41	59	47	53

Nombres jamais somme de deux premiers

Ce sont des nombres impairs (cf. Goldbach !)

1, 2, 3, 11, 17, 23, 27, 29, 35, 37, 41, 47, 51, 53, 57, 59, 65, 67, 71, 77, 79, 83, 87, 89, 93, 95, 97, 101, 107, 113, 117, 119, 121, 123, 125, 127, 131, 135, 137, 143, 145, 147, 149, 155, 157, 161, 163, 167, 171, 173, 177, 179, 185, 187, 189, 191, 197, 203, 205, 207, 209, 211, 215, 217, 219, 221, 223, 227, 233, 237, 239, 245, 247, 249, 251,

Records de quantités de partitions en deux premiers pour n de 1 à 1000

[Nombre n, Quantité de partitions en deux nombres premiers]

[4, 1], [10, 2], [22, 3], [34, 4], [48, 5], [60, 6], [78, 7], [84, 8], [90, 9], [114, 10], [120, 12], [168, 13], [180, 14], [210, 19], [300, 21], [330, 24], [390, 27], [420, 30], [510, 32], [630, 41], [780, 44], [840, 51], [990, 52].

Nombres somme de trois premiers (1 à 50)

n = p1 + p2 + p3 = q1 + q2 + q3…

En jaune, record de multi-partitions

n	p1, p2, p3	q1, q2, q3	Etc.
1
2
3
4
5
6	2, 2, 2
7	2, 2, 3
8	2, 3, 3
9	2, 2, 5	3, 3, 3
10	2, 3, 5
11	2, 2, 7	3, 3, 5
12	2, 3, 7	2, 5, 5
13	3, 3, 7	3, 5, 5
14	2, 5, 7
15	2, 2, 11	3, 5, 7	5, 5, 5
16	2, 3, 11	2, 7, 7
17	2, 2, 13	3, 3, 11	3, 7, 7	5, 5, 7
18	2, 3, 13	2, 5, 11
19	3, 3, 13	3, 5, 11	5, 7, 7
20	2, 5, 13	2, 7, 11
21	2, 2, 17	3, 5, 13	3, 7, 11	5, 5, 11	7, 7, 7
22	2, 3, 17	2, 7, 13
23	2, 2, 19	3, 3, 17	3, 7, 13	5, 5, 13	5, 7, 11
24	2, 3, 19	2, 5, 17	2, 11, 11

25	3, 3, 19	3, 5, 17	3, 11, 11	5, 7, 13	7, 7, 11
26	2, 5, 19	2, 7, 17	2, 11, 13
27	2, 2, 23	3, 5, 19	3, 7, 17	3, 11, 13	5, 5, 17
	5, 11, 11	7, 7, 13
28	2, 3, 23	2, 7, 19	2, 13, 13
29	3, 3, 23	3, 7, 19	3, 13, 13	5, 5, 19	5, 7, 17
	5, 11, 13	7, 11, 11
30	2, 5, 23	2, 11, 17
31	3, 5, 23	3, 11, 17	5, 7, 19	5, 13, 13	7, 7, 17
	7, 11, 13
32	2, 7, 23	2, 11, 19	2, 13, 17
33	2, 2, 29	3, 7, 23	3, 11, 19	3, 13, 17	5, 5, 23
	5, 11, 17	7, 7, 19	7, 13, 13	11, 11, 11
34	2, 3, 29	2, 13, 19
35	2, 2, 31	3, 3, 29	3, 13, 19	5, 7, 23	5, 11, 19
	5, 13, 17	7, 11, 17	11, 11, 13
36	2, 3, 31	2, 5, 29	2, 11, 23	2, 17, 17
37	3, 3, 31	3, 5, 29	3, 11, 23	3, 17, 17	5, 13, 19
	7, 7, 23	7, 11, 19	7, 13, 17	11, 13, 13
38	2, 5, 31	2, 7, 29	2, 13, 23	2, 17, 19
39	3, 5, 31	3, 7, 29	3, 13, 23	3, 17, 19	5, 5, 29
	5, 11, 23	5, 17, 17	7, 13, 19	11, 11, 17	13, 13, 13
40	2, 7, 31	2, 19, 19
41	2, 2, 37	3, 7, 31	3, 19, 19	5, 5, 31	5, 7, 29
	5, 13, 23	5, 17, 19	7, 11, 23	7, 17, 17	11, 11, 19
	11, 13, 17
42	2, 3, 37	2, 11, 29	2, 17, 23
43	3, 3, 37	3, 11, 29	3, 17, 23	5, 7, 31	5, 19, 19
	7, 7, 29	7, 13, 23	7, 17, 19	11, 13, 19	13, 13, 17
44	2, 5, 37	2, 11, 31	2, 13, 29	2, 19, 23
45	2, 2, 41	3, 5, 37	3, 11, 31	3, 13, 29	3, 19, 23
	5, 11, 29	5, 17, 23	7, 7, 31	7, 19, 19	11, 11, 23
	11, 17, 17	13, 13, 19
46	2, 3, 41	2, 7, 37	2, 13, 31
47	2, 2, 43	3, 3, 41	3, 7, 37	3, 13, 31	5, 5, 37
	5, 11, 31	5, 13, 29	5, 19, 23	7, 11, 29	7, 17, 23
	11, 13, 23	11, 17, 19	13, 17, 17
48	2, 3, 43	2, 5, 41	2, 17, 29	2, 23, 23
49	3, 3, 43	3, 5, 41	3, 17, 29	3, 23, 23	5, 7, 37
	5, 13, 31	7, 11, 31	7, 13, 29	7, 19, 23	11, 19, 19
	13, 13, 23	13, 17, 19
50	2, 5, 43	2, 7, 41	2, 11, 37	2, 17, 31	2, 19, 29

Records de quantités de partitions en trois premiers pour n de 1 à 500

[Nombre n, Quantité de partitions en trois nombres premiers]

[6, 1], [9, 2], [15, 3], [17, 4], [21, 5], [27, 7], [33, 9], [39, 10], [41, 11], [45, 12], [47, 13], [51, 15], [53, 16], [57, 17], [63, 19], [65, 21], [71, 22], [77, 28], [83, 29], [89, 33], [95, 35], [101, 38], [107, 43], [113, 47], [119, 50], [125, 53], [131, 57], [137, 62], [143, 65], [149, 68], [155, 69], [161, 77], [167, 78], [173, 89], [185, 92], [191, 95], [197, 102], [203, 107], [209, 110], [215, 116], [221, 122], [227, 125], [233, 130], [239, 132], [245, 134], [251, 142], [257, 154], [269, 157], [275, 158], [277, 160], [281, 171], [287, 176], [293, 186], [299, 187], [305, 190], [311, 198], [317, 210], [335, 213], [341, 234], [347, 237], [353, 244], [371, 254], [377, 267], [383, 278], [401, 287], [407, 294], [413, 300], [425, 304], [431, 318], [437, 336], [461, 352], [467, 369], [473, 373], [479, 377], [491, 388], [497, 394].

Accès à chacun des nombres de cette page via le DicoNombre

Retour	Conjecture de Goldbach Tables – Index
Suite	Formulations, variantes et historiques Partitions
Voir	Conjecture – Glossaire Bi, tripartitions Fermat Modulo & Congruences Nombres Premiers Sommes de nombres premiers consécutifs
Sites	OEIS 109679 – Smallest even number which is the unordered sum of two primes in more ways than any previous even number. OEIS A139322 – Record values of n in A068307 OEIS A068307 - From Goldbach problem: number of decompositions of n into a sum of three primes
Cette page	http://villemin.gerard.free.fr/ThNbDemo/GoldbaTa.htm