|
Édition du: 22/06/2025 |
Faites un double-clic pour un retour en haut de page
![]()
|
PAVAGE FINI du plan
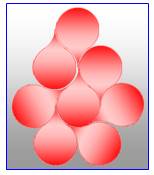
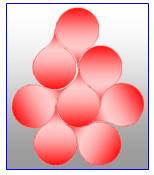
Pavage en
couronne autour d'un motif de base. En principe avec une seule tuile (ou
pavé) posée à l'endroit ou à l'envers. Bien évidemment sans espace vide et
sans chevauchement. Le nombre
de Heesch indique la quantité maximale de couronnes réalisables autour d'une
tuile sans possibilité d'en ajouter un autre. Le nombre de Heesch le plus
grand connu en fin 2023 est 6. Figure: pavage avec deux couronnes. Nombre de Heesch
1. |
||
|
|
Sommaire de cette page >>> Types de pavages >>> Pavage fini |
Débutants Glossaire |
Anglais: Tiling or
tessallation
|
Types de pavages Le problème du pavage du plan est un vaste
domaine d'études. On distingue au moins trois grandes familles de pavage.
Pour chacun des pavages, on peut utiliser une
tuile ou plusieurs tuiles; toutes dans le même sens ou retournement autorisé. Les formes des tuiles peuvent être droites (polygones
réguliers ou non) ou courbes. |
Pavage infini périodique avec une tuile
ou deux tuiles
Pavage apériodique
|
|
|
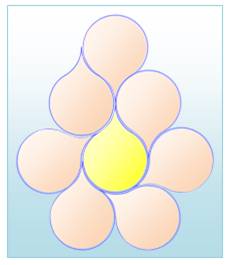
Fini Le principe consiste à poser une tuile et, avec le
même type de tuile, à l'endroit ou à l'envers, à faire le tour de la
première. En fait, il s'agit de créer une sorte de couronne autour de la
première tuile. S'il est possible de créer cette couronne, sans
qu'il soit possible de créer une nouvelle couronne, le nombre de Heesch de la
tuile est 1. Nombre de Heesch C'est tout simplement la quantité de couronnes
qu'il est possible de réaliser avec une tuile donnée, sans pouvoir créer une
couronne supplémentaire. Le nombre de Heesch d'un pavage périodique est
infini. Celui de la tuile circulaire est 0. H = 1 – 1928: Walter Lietzmann – Goutte d'eau H = 1 – 1968: Henrich Heesch – Hexagone H = 2 – 1991: Anne Fontaine H = 3 – 1990-1995: Robert Ammann H = 4 – 2001: Casey Mann H = 5 – 2001: Casey Mann H = 6 – 2020: Bojan Basic H = 7 – Inconnu en fin 2023 Voir Dessin
des tuiles Heinrich Heesch
(1906-1995), mathématicien allemand, expert en théorie des graphes (quatre
couleurs). |
Tuile en forme d'un F: H = 0
Tuile en forme d'un H allongé
Oups! Il est possible de continuer à créer des
couronnes. Tuile en goutte d'eau: H = 1
|
|
Voir Brève
56-1119
Rectangle 5×7 avec encoches: H = 1

Auteur: Erich
Friedman
Haut de page (ou
double-clic)
![]()
|
Suite |
||
|
Voir |
|
|
|
Article |
|
|
|
Sites |
|
|
|
Cette page |
||