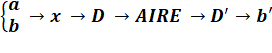|
Édition du: 25/07/2022 |
|
INDEX |
Carrés: énigmes et paradoxes |
||
|
Carré
inscrit (Toeplitz) |
|||
Faites
un double-clic pour un retour en haut de
page
![]()
|
Paradoxe du carré manquant (Lewis Carroll) Découpage d'un carré
(ou rectangle).
Curieusement en réunissant les pièces d'une autre façon, il existe un trou,
un carré manquant. |
||
|
|
Sommaire de cette page >>> Puzzle- Le
carré >>> Explications >>> Puzzle – Le
triangle >>> Puzzle – Dans
le carré |
Débutants Glossaire |
|
LEWIS CARROLL Charles Lutwidge Dodgson, pseudonyme Lewis Carroll
(1832-1898) Célèbre pour la
création du personnage: Alice, soumise à des situations
déconcertantes "Alice in Wonderland" Alice au pays des
merveilles |
|
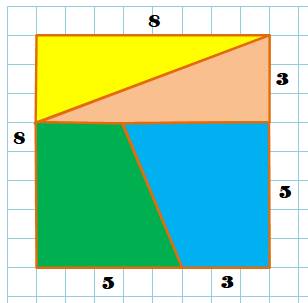
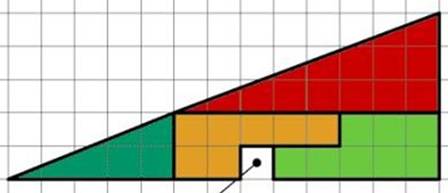
Construction Prenons
un carré de 8 x 8. Découpons
deux triangles rectangles
et deux trapèzes comme
indiqué. Nous nous proposons de transformer ce carré en rectangle à l'aide de
ces quatre
pièces; la solution n'est pas bien difficile Seulement voilà, il y a un air (ou une aire) de mystère! |
|
||
|
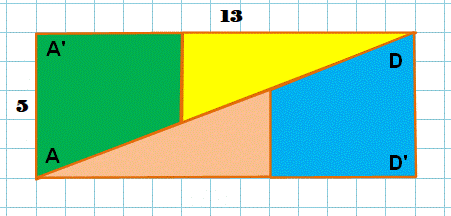
Aire du carré: 8 x 8 = 64 Aire du rectangle: 13 x 5 = 65. Nous avons réussi à créer une surface plus grande d'une unité. Où est
ce mystère? Dans le dessin de la diagonale AD. |
|
||
|
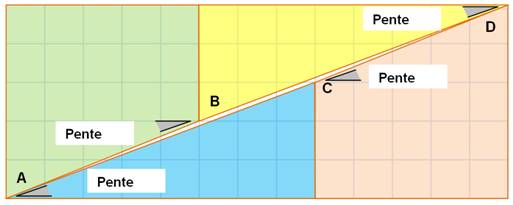
Diagonale ? Calculons la pente des segments qui forment la diagonale: p AB = p CD = 2 / 5 = 0,4 p BD = p AC = 3 / 8 = 0,375 p AD = 5 / 13 = 0,384 |
|
||
|
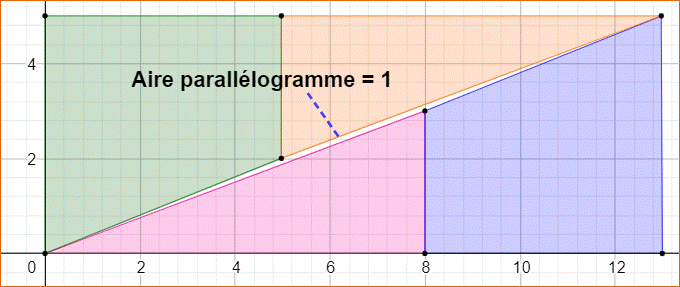
Ces
pentes sont toutes différentes! Un dessin
précis montre qu'il existe un petit jour en forme de parallélogramme très
effilé le long de la diagonale. |
On remarque que les nombres donnant la dimension
des pièces (3, 5, 8 et 13) constituent une suite de Fibonacci
(impliquant aussi le nombre d'or,
Phi) Pour des nombres de Fibonacci plus grands, la
différence serait encore plus difficile à discerner, (le parallélogramme
serait encore plus effilé) car ils donneraient une meilleure approximation de
Phi. |
||
Dessin précis avec
GeoGebra
|
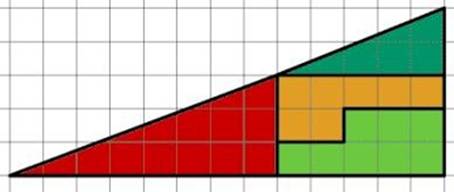
Construction Avec les
mêmes nombres de Fibonacci (3, 5, 8 et 13), on peut former des triangles
paradoxaux, et mettre en valeur l'aire unité qui flotte. |
Carré manquant |
||||||||||
|
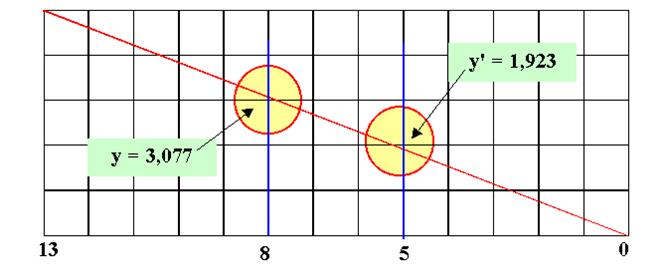
Explication Le dessin
montre que la diagonale ne passe pas par un point de la grille pour x = 5 et
pour x = 8. Donc un
découpage fallacieux au départ !
Calcul des ordonnées des points
indiqués
|
|||||||||||
|
Paradoxe Avec le
même découpage en carrés et triangles formant un carré, un nouvel assemblage recomposant
le carré fait apparaitre un trou carré. Explication
? Comme
précédemment, les dimensions sont proches mais pas exactement les mêmes. |
|
||
|
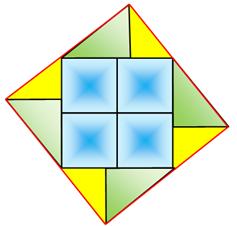
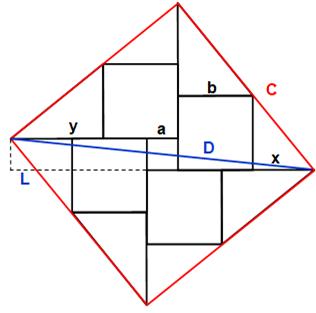
Explications On prend l'aire du carré comme invariant. En se donnant a et b pour la seconde figure et, via
l'aire commune, on va en déduire la valeur de b' dans la première figure. Il nous faudra d'abord connaitre la taille des
triangles rectangles (valeur de x). |
Résumé de la recherche
|
||
|
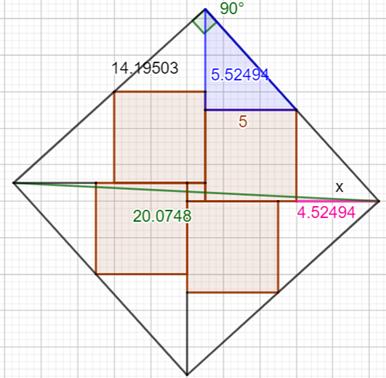
Valeur de x
Longueur de la diagonale D et AIRE
Valeur de b'
|
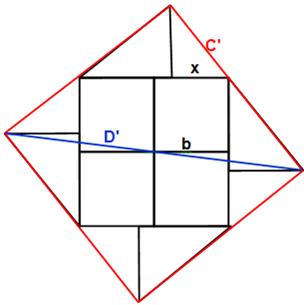
Figures et notations
Conclusion Pour conserver l'aire du grand carré, avec b = 5
dans la figure du haut, b devient 5,02dans la figure du bas. Pour info, longueurs des diagonales: D ≈ 20,074 D' ≈ 20,022 |
||
|
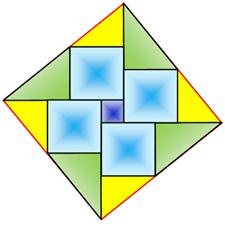
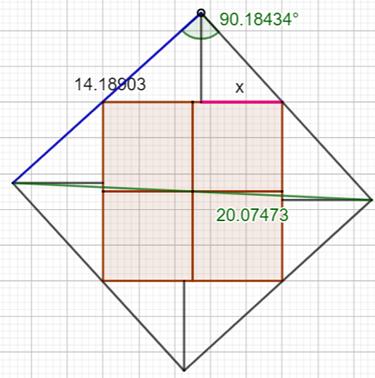
Illustration de la différence Cette fois on ne garde pas l'aire constante comme ci-dessus. Ce sont les
douze pièces qui sont intégralement
conservées. Dessin avec Geogebra. Figure du haut On construit la figure du haut en premier. Carré central avec a = 1 et quatre carrés qui
l'entourent avec b = 5. On prolonge un côté de carré d'une longueur égale
à x exactement (formule avec la racine). Et cela quatre fois. Les extrémités sont reliées pour former un
quadrilatère. C'est évidemment un carré (la valeur de x a été
calculée pour cela) Figure du bas Cette figure est composée des mêmes pièces que
celles du carré d'en-haut, rigoureusement. Quatre carrés adjacents. Report de la valeur exacte de x sur le côté d'un
carré, et cela quatre fois. Perpendiculaire en ces quatre points et point à
une distance de 5. Ces quatre points sont les sommets d'un
quadrilatère. Ce n'est pas un carré: un des angles dépasse 90°. |
|
Voir Brève
889
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |