NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 03/03/2021 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Pavage
Débutants Géométrie	Avec des DOMINOS			Glossaire Géométrie
INDEX Géométrie Jeux	Dominos	Pavage Fibonacci	Pavage sans faute	Échiquier
		Sommaire de cette page >>> Principe du pavage >>> Cas de n= 3 >>> Cas n = 1 à 4 >>> Bilan >>> Rectangles 1 x n >>> Énigmes de pavages avec dominos

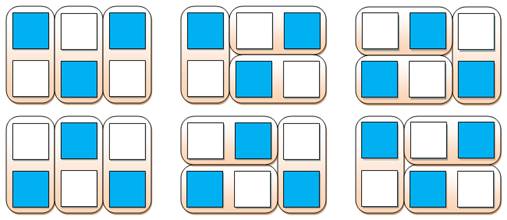
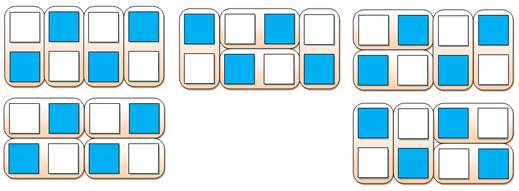
Pavage du RECTANGLE

avec des DOMINOS

Et les Fibonacci surgissent …

Voir Pavage – Une approche via les transformations

Principe du pavage
Le rectangle est un damier de dimension 2 x N Le domino est formé de deux carrés bicolores; peut importe sa valeur. Le pavage consiste à placer les dominos sur le rectangle d'autant de façons que possible. Une contrainte est ajoutée: les extrémités des dominos doivent être de couleurs différentes. Combien de combinaisons possibles selon la valeur de N?

Cas de N = 3
Voici six cas. Chaque dessin du dessous est, en fait, celui du haut tourné d'un demi-tour. Ils ne sont pas comptés. Le compte des combinaisons est donc: C = 3.

Cas N = 1 à 4
N = 1; C = 1 N = 2; C = 2 N = 3; C = 3 N = 4; C = 5	Rappel: le damier mesure 2 x N

Bilan
La quantité de combinaison forme la suite des nombres de Fibonacci. La quantité à chaque itération est égale à la somme des quantités des deux fois précédentes. Exemple: 5 = 3 + 2.

Rectangle 1 x n
En dénombrant les possibilités de paver le rectangle de largueur unité, voici à nouveau les nombres de Fibonacci qui font leur apparition.

Voir Brève 622

Énigmes de pavages avec dominos
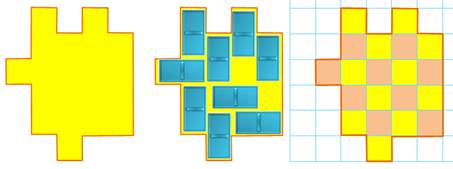
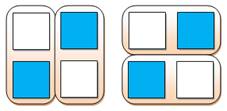
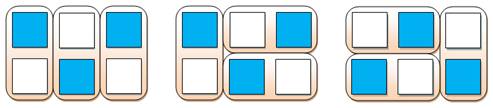
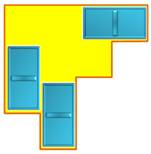
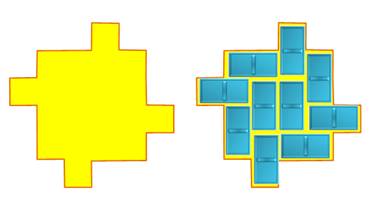
L'énigme la plus classique est celle du pavage de l'échiquier. Pour commencer et s'exercer, comment paver la forme 1 ? L'idée consiste à commencer par positionner les dominos qui ne peuvent prendre qu'une seule position. Ici, la suite est évidente. Le pavage de la forme 2 n'est pas très compliqué non plus. Que penser de la forme3 ? Tentative vaine, le pavage avec dominos est impossible. Un domino se pose sur deux cases de couleurs différentes. Or, ici nous avons 11 jaunes et 9 roses.	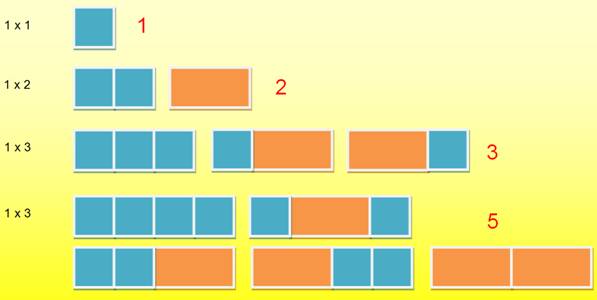Forme 1 Forme 2 Forme 3

Voir Énigmes et puzzles – Index

Suite	Pavage minimal Carré et rectangle à trou Dominos Échiquier et dominos Hexagone – pavage Polygone – pavage
Voir	Carré Carrés parfaits Construction géométrique des nombres Dodécagone Géométrie – Index Hexagone – Généralités Méandres Pavage mystérieux du triangle Pentominos Poincaré Polygone Triangle équilatéral
Cette page	http://villemin.gerard.free.fr/Pavage/Domino.htm