|
|||||||||||||||||||||||||||||||||||
![]()
|
GOLYGONE Isogone à 90° sériel Polygone à angles droits dont les côtés mesurent successivement les nombres entiers de 1 à n. Inventés par Lee Sallows en 1988 et popularisés
en 1990 par Alexander Dewdey dans un article du Scientific American. Leur
étude a été menée conjointement par quatre éminents mathématiciens: Lee
Swallows, Martin Gardner, Richard Guy et Donald Knuth. |
Anglais: Golygons, serial isogons
|
|
||
|
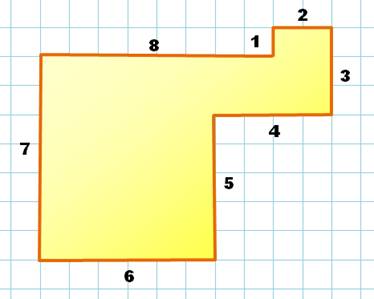
Il est inscrit dans un rectangle de 10 x 8.
|
Golygone à huit côtés
Sommes des longueurs des côtés 1 – 3 – 5 + 7 = 0; 1 + 3 + 5 + 7 = 16 = 4² 2 – 4 – 6 + 8 = 0; 2 + 4 + 6 + 8 = 20 = 4 x 5 Pavage du plan avec les golygones (n = 8)
|
|
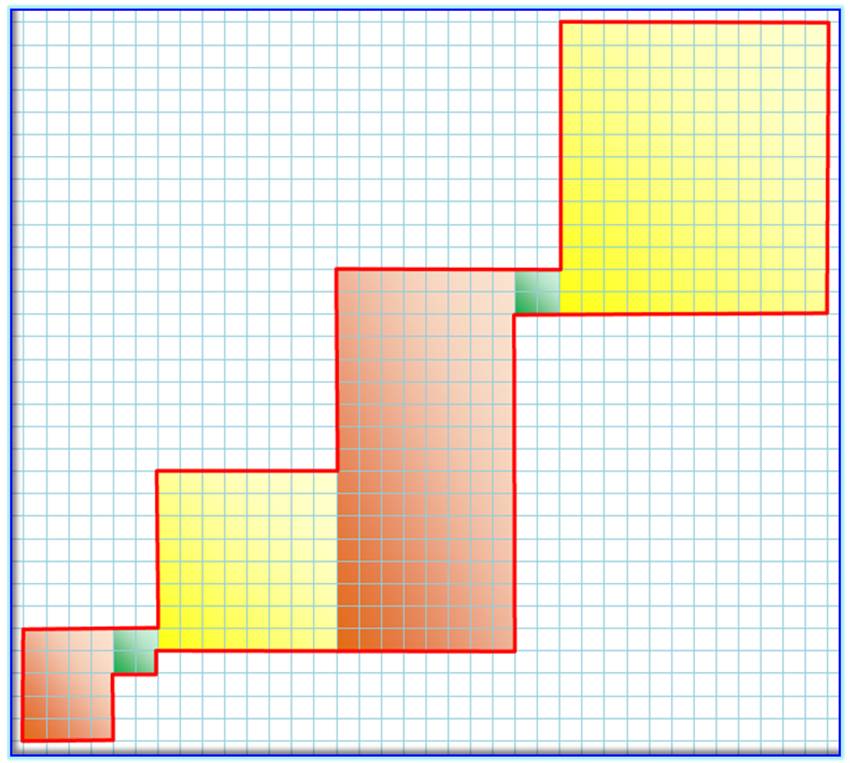
Un
golygone d'ordre 2 (16 côtés) – Rectangle 32 x 36
|
|
||
|
|
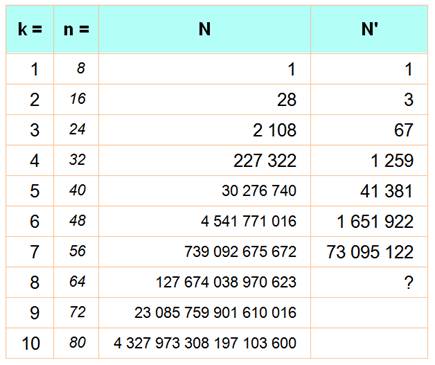
n = 8k ? |
|
|
|
n = 2m |
|
|
|
Sv =
1 + 3 + … 2m – 1 = m² |
|
|
|
m² est pair et m est pair. |
|
|
|
SH =
2 + 4 + … + 2m = m (m + 1) |
|
|
|
SHD =
SHG = ½ m (m + 1) = 2a m (m + 1) est divisible par 4 |
|
|
|
Or m est pair Donc m + 1 est impair |
|
|
|
m est divisible
par 4 |
|
|
|
n est divisible
par 8. N = 8k |
|
|
|
|
|
|
|
|
|
||
|
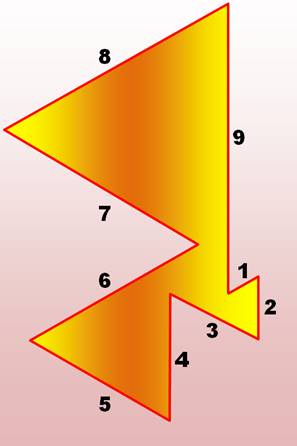
Exemple à neuf
côtés. Le plus petit avec n =>
|
|
|
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Articles |
Promenades carrées et
cubes collés
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/GeomLAV/Polygone/Golygone.htm
|
![]()