|
|||||||||||||||||||||||||||||
![]()
|
NOMBRES MÉANDRIQUES Pour un nombre donné
d'intersections entre deux courbes, dénombrer les cas de figures possibles.
Un sujet de combinatoire
avec un petit air de topologie. |
Anglais: Meandric number
|
|
||
|
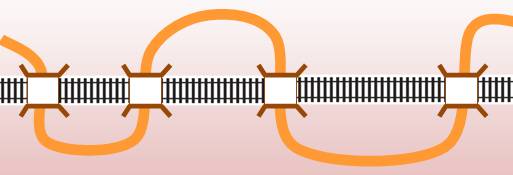
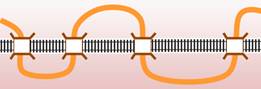
Une analogie: une
voie ferrée rectiligne et la route qui la croie et recroise …
|
||
|
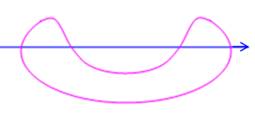
Deux courbes qui
tricotent. Exemple Ici les deux courbes sont ouvertes. Il y a 3 points d'intersection. |
|
|
|
On prend l'habitude
de considérer une des courbes comme une ligne
droite, ce qui ne change rien du point de vue topologique (homéomorphisme). Quant à l'autre,
elle peut être: ouverte ou fermée. |
|
|
|
Notes Aucune des deux ne se
recoupe elle-même. Les figures obtenues par déformations
"légères" de la courbe sont
considérées comme semblables. |
||
|
En gros, ça veut dire que c'est la même forme, via une
déformation continue. Comme un tore
et une tasse munie une anse. Une sorte de transformation avec pâte à
modeler. C'est une application bijective
continue. Une
application f de l'espace topologique X dans l'espace topologique Y est
appelée un homéomorphisme si elle est
bijective et si elle est continue ainsi que son inverse. Il est important de
noter qu'une application bijective et continue n'est pas nécessairement un
homéomorphisme. Dans le cas des méandres,
seul les intersections comptent; les deux courbes en jeu peuvent être
déformées tant que les intersections sont conservées. |
Voir Homéomorphisme
en topologie
|
|
|||
|
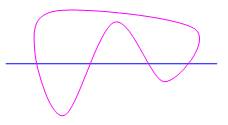
Méandres ouverts Dans le cas d'une
courbe ouverte, on compte la quantité d'intersections. Soit quatre sur cette
illustration. Les deux lignes sont orientées |
|
||
|
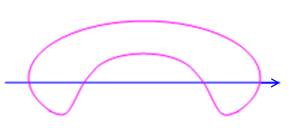
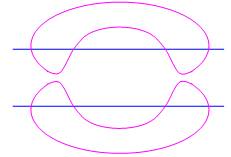
Méandres fermés Dans le cas d'une
courbe fermée:
Exemple Ici les deux
paires de points d'intersection. Combien existe-t-il
de figures présentant deux paires de points ? On dit que la
figure est d'ordre 2: 2 paires de points d'intersection. Et que le nombre
méandrique est 2: 2 figures distinctes possibles. |
M2 = 2 |
||
|
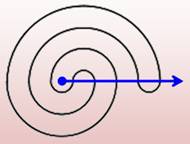
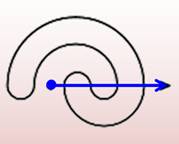
Semi-méandres Dans ce la courbe
est fermée et la droite est en fait une demi-droite. On compte le nombre
d'enroulements (de tours) autour du point d'origine. |
5 intersections 4
intersections 3 tours 0
tour |
||
|
Arches Quantité de paires
de pieds de courbes situées d'un côte de la ligne droite |
4 arches |
||
|
|
|||
|
Ordre 1 |
M1 = 1 |
|
|
|
Ordre 2 |
M2 = 2 |
On sous-entend que
la ligne droite est orientée de gauche vers la droite. De ce point de vue,
ces dux figures sont différentes. |
|
|
Ordre 3 |
M3 = 8 |
|
|
|
Les douze premiers nombres méandiques |
|
||
|
|
|||
|
Un peu de théorie La théorie des
méandres appartient à la combinatoire. Elle cherche à
dénombrer la quantité de types de courbes qui coupent une droite selon un nombre de points d'intersection
donné. Le dénombrement des
méandres est un problème
non résolu. Poincaré s'est intéressé à ces problèmes. |
Trois catégories de méandres
Le problème se
complique encore en introduisant les multi-boucles!
|
||
|
Nombre méandrique Un méandre fermé
d'ordre n est une courbe fermée sans intersection avec elle-même qui a 2n
points d'intersection avec une droite donnée. Le nombre
méandrique Mn comptabilise la quantité de cas de figures possibles pour
chaque ordre. On pense que: Mn
croît exponentiellement Mais aucune
formulation n'est connue. On en cherche une approximation. |
|
||
Table des trois sortes de nombres
méandriques
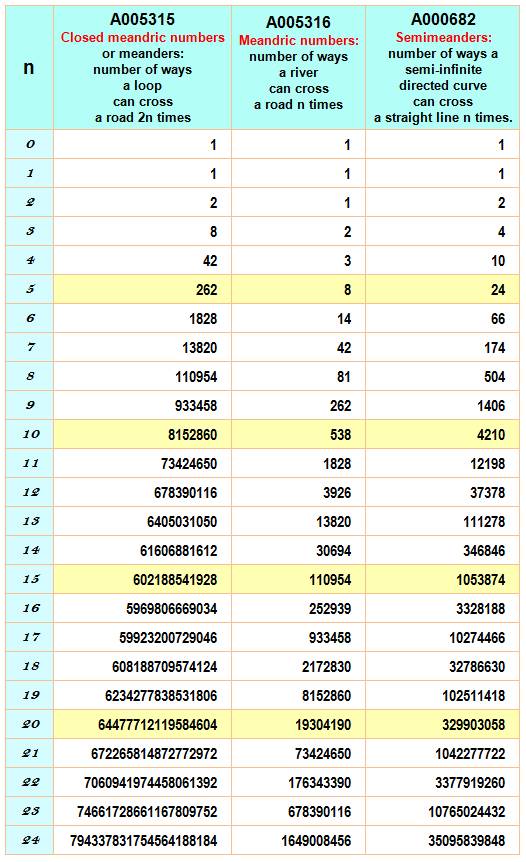
Voir Tables – Index
|
Meanders are combinatorial objects with a topological flavour, encapsulating properties of
the interplay between planarity and connectedness. They correspond to the
systems formed by the intersections of two curves in the plane, with
equivalence up to homeomorphism within
the plane. |
![]()
|
Suite |
|
|
Voir |
|
|
Site |
|
|
Cette page |
![]()