|
Édition du: 23/06/2025 |
|
INDEX |
Dissections |
||
|
Carré-Triangle
équilatéral (problème du mercier) |
|||
Faites un double-clic pour un retour en haut de page
![]()
|
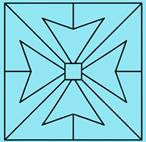
Comment
découper la croix de Malte pour assembler les morceaux en un carré. C'est la quadrature
de la croix de Malte ou encore la dissection de la croix en carré.
Sur cette
page deux dissections: la croix de Malte classique et une croix modifiée. |
||
|
|
Sommaire de cette page >>> Croix de Malte (classique) >>> Croix de Malte modifiée |
Débutants Glossaire |
|
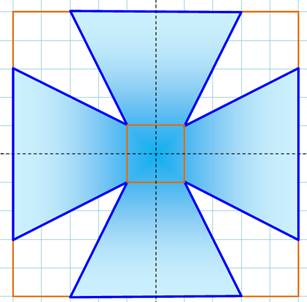
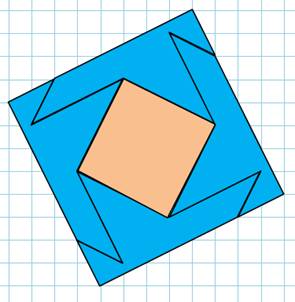
Croix de malte modifiée La
croix est constituée de quatre branches. Les
dimensions sont repérables sur le quadrillage de la figure. Notez
que si le carré intérieur est unitaire, le
carré circonscrit à la croix est cinq fois supérieur. Toute la croix est
dessinée dans un quadrillage de 5 x 5 (ou 10 carreaux par 10 carreaux). Dissection en carré Le
but est de partager la croix en huit parties telles que celles-ci puissent être
assemblées en un carré, sans trou et sans chevauchement. Idée Avoir
l'intuition du découpage n'est pas évident.
La
suite reste une question d'intuition et de réflexion. Le découpage indiqué à
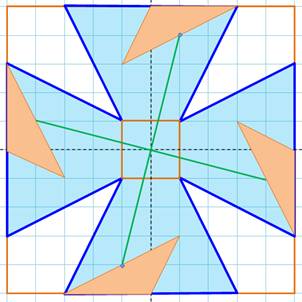
été proposé par Bernard Lemaire. Découpe Les
triangles ont pour sommet un des sommets de la croix, le point milieu de la
croix et un point du quadrillage unitaire. La
seconde pièce octogonale vient en traçant les sortes de diagonales vertes qui
joignent les milieux des côtés des triangles. Les angles droits au centre
forment les quatre angles droits du carré final. Assemblage Chaque
pièce bleue est translatée de l'autre côté du carré central. Ces pièces s'emboitent
deux à deux et laissent des espaces triangulaires où viennent se loger les
quatre triangles ocres. |
|
|
Voir Brève
63-1247
|
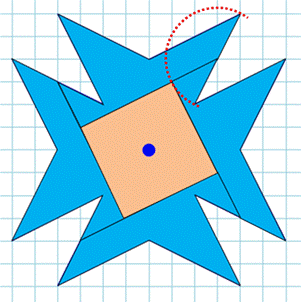
Croix de malte modifiée La
croix est constituée de quatre branches dont les extrémités sont formées de
deux demi-branches concaves. Les
dimensions sont repérables sur le quadrillage de la figure. Dissection en carré Le
but est de partager la croix en cinq parties telles que celles-ci puissent être
assemblées en un carré, sans trou et sans chevauchement. Idée Avec
cinq pièces, on n'image peu cinq pièces identiques avec des cinquièmes de rotation. On
imagine plutôt quatre pièces identiques et une cinquième qui couvrirait un
espace carré. Découpe Les
côtés du carré central sont parallèles aux demi-branches de la croix, une sur
deux. Les
côtés du carré sont prolongés pour former quatre polygones identiques. Propriété Le
prolongement et les demi-branches ont
même longueur (cercle en pointillé rouge). Propriété indispensable pour
réaliser l'assemblable final en carré. Assemblage Chaque
pièce bleue est translatée de l'autre côté du carré. Ces pièces s'emboitent
deux à deux et laissent un espace carré au centre. Le carré ocre y trouve
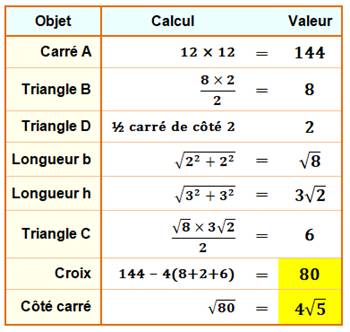
exactement sa place. Mesures L'aire
de la croix se calcule et donne: 80 De
sorte que le carré de même aire a un côté de: Historique et références Cette
dissection est parue en 1972 chez Dover par Gerg Frederickson On
trouve des animations de ces dissections par
Bernard Lemaire sur Internet. |
|
|
|
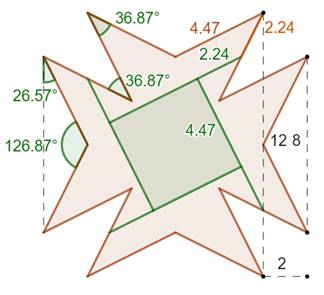
Calcul du côté du carré final
|
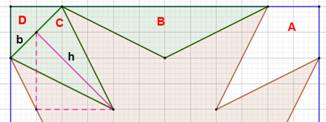
Notations pour les calculs
Principales mesure sur la croix
|
Haut de page (ou
double-clic)
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
|
|
|
Cette page |