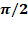|
Édition du: 15/12/2024 |
|
INDEX |
Dérivées |
|||
Faites un double-clic pour un retour en haut de page
![]()
|
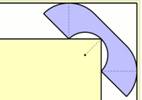
Passage du Sofa dans un angle
Comment
faire passer un sofa dans couloir présentant un angle droit. Résolu
par Jineon Baek en fin 2024. |
||
|
|
Sommaire de cette page >>> Cas général du sofa >>> Cas particulier de la planche |
Débutants Glossaire |
Anglais: Moving sofa problem
Passage
du sofa
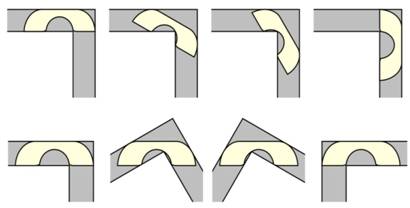
Crédit arXiv
(2024)
Cas général du sofa ou canapé |
||
|
Problème du sofa Problème formalisé par le mathématicien Leo Moser
(austro-canadien) en 1966. Trouver la forme rigide plane d'aire maximale que
l'on peut déplacer dans un couloir d'un mètre
de large avec un angle droit (en forme de L). Problème non résolu. Solution simple Sofa demi-circulaire de rayon unité. L'aire est alors égale à: Hammersley donne une limite supérieure: Constante du sofa = aire maximale du sofa Elle est comprise entre:
Solution trouvée en fin 2024 Jineon Baek (Université Yonsei, Corée) repart de
la forme du canapé mis au point par Joseph Gerver. Il démontre que la surface
maximale possible du canapé est bien celle que Gerver avait trouvée au
départ, c’est-à-dire 2,2195
unités. Sa solution doit encore être vérifiée par ses
pairs. |
Solution de John Hammersley (1968) Un demi-cercle de rayon unité, coupé en deux, augmenté
d'un rectangle intermédiaire, lequel est évidé d'un demi-cercle. Aire:
Source image: Wikipédia |
|
Voir Brève
45-898 / Actualités 2024
|
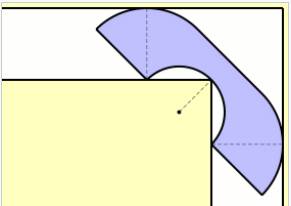
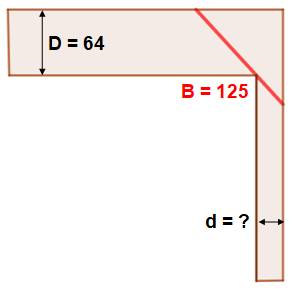
Construction du couloir en L Un couloir de largueur D = 64 cm et un retour de
largueur d à déterminer. Quelle est celle largueur minimale permettant de
faire passer une planche très large et de longueur B = 125 cm d'un couloir à
l'autre. Se problème se ramène à un problème dans le plan
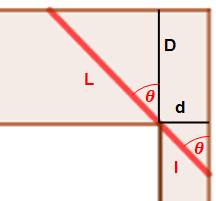
tel que représenté sur cette figure. Piste (figure du bas) En traçant les deux segments noirs, on forme deux
triangles rectangles semblables. La planche est formée des deux morceaux L et l dont
on peut calculer la longueur avec les sinus
ou cosinus de l'angle téta. Alors, reste à minimiser la largeur d. C'est
possible en cherchant la racine de la dérivée
(le passage par zéro de la fonction dérivée). On se souvient
que (la dérivée étant notée '): |
|
|
|
Calculs
|
Vérification
|
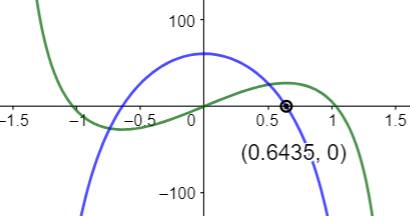
Tracé obtenu par GeoGebra En vert la fonction et en bleu sa dérivée: Le point d'intersection avec l'axe des x est en
0,6435. Ce qui est la valeur en radian de l'angle
optimum. Son cosinus vaut 0,8 = 4/5. |
|
Haut de page (ou
double-clic)
![]()
|
Retour |
|
|
|
Suite |
|
|
|
Voir |
|
|
|
Sites |
|
|
|
Cette page |
||