Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 06/11/2024 M'écrire Brèves de Maths

Débutant Glossaire Types de nombres Nombres géométriques Nom des nombres Écriture des nombres Table des facteurs Nombres et anglais Langues	Dictionnaire des Nombres
	1 / 10 / 50 / 60 / 70 / 75 / 76 / 77 / 78 / 79 / 80 / 81 / 82 / 83 / 84 / 85 / 86 / 87 / 88 / 89 / 90 / 91 / 92 / 93 / 94 / 95 / 96 / 97 / 98 / 99 / 100	101	102 /103 / 104 / 105 / 106 / 107 / 108 / 109 / 110 / 115 / 120 / 130 / 140 / 150 / 200 / 250 / 300 / 400 / 500 / 1000 / Autres

Nombre 101

Expressions 101

Nombre 1/101

Nombre 10101 …

Cent-un

One hundred (and) one

Orthographe / Langues

Facteurs
Diviseurs	1, 101
Quantité	2
Somme	102
Binaire	110 0101
Romain	CI

Suite en propriétés arithmétiques

Langues

Français cent-un, cent-unième Suite >>>

Anglais one hundred (and) one

Allemand (ein)hundert(und)eins

Espagnol ciento un(o)

Italien cent(o) un

Orthographe des nombres

Nombres dans toutes les langues

Congruent primitif (lent)

Déficient

Dihédral

Docile

Erdös

Glissant

Impair

Jonction

Jumeau avec 103, cousin avec 97 et sexy avec 107

Mertens nul

Nombre jonction

Partition (de 13)

Premier (26^e)
Premier bon

Premier de Chen

Premier de Pythagore

Premier de Ramanujan

Premier fort

Premier irrégulier

Premier irrégulier d'Euler

Premier oscillant

Premier pointé

Premier unique

Géométrique

Décagonal centré (5^e)

Dihédral

Palindrome

Strobogrammatique

Tétradique

101 – Général

Langue	A hundred and one things to do – Tant de choses à faire.	>>>
Cinéma	Les Cent Un Dalmatiens Walt Disney – 1961 – One Hundred and One Dalmatians	>>>
Chimie	N° 101 = Mendélévium découvert en 1955	>>>
Géographie	Mayotte est le 101^e département français depuis 2010	>>>
Politique	101 coups de canon: mort d'un monarque et investiture de son successeur	>>>

101 – Nombre

Chiffres et numération

		Stobogrammatique et palindrome.
101 et 787	Seuls nombres premiers à avoir des chiffres en n, n+1, n.
101	Nombre holodifférence: tout chiffre est la différence de deux autres. Les suivants à trois chiffres: 101, 110, 202, 220, 303, 330, 404, 440, 505, 550, 606, 660, 707, 770, 808, 880, 909, 990. Soit, tous les nombres avec deux chiffres répétés et un zéro.
101 = 10² + 1²	Les chiffres des deux nombres se retrouvent dans la somme de leurs carrés
101 et 103 sont jumeaux 101 + (1+0+1) = 103			Séquence typique de jumeaux et de cousins: 97, 101, 103, 107, 109, 113. Devient le nombre premier suivant en lui ajoutant ses chiffres.
101, 103, 107 101, 103, 107, 109 101, 103, 107, 109, 113			Triplet de premiers pointés. On passe au suivant en ajoutant les chiffres du précédent. Le deuxième plus petit tel triplet. Deuxième quadruplet de premiers dans une dizaine. Quintuplet de premiers.

Addition et soustraction

		Nombre glissant.
101 – 1! = 101 – 1 = 100 101 – 2! = 101 – 2 = 99 101 – 3! = 101 – 6 = 95 101 – 4! = 101 – 24 = 77	Ce nombre, diminué des factorielles inférieures, produit des nombres composés.
101 = 91 + 9 + 1 = 100 + 1	Le plus petit nombre jonction.
101 = 13 + 17 + 19 + 23 + 29	Somme de nombres premiers consécutifs.
101 = 5! – 4! + 3! – 2! +1!	Factorielle alternée.
101 – 1 = 100 101 – 2 = 99 101 – 6 = 95 101 – 24 = 77	Nombre d'Erdös: le nombre premier reste composé en le diminuant des factorielles qui lui sont inférieures. Liste de tels nombres: 101, 211, 367, 409, 419, 461, 557, 673, 709, 937, 967, … OEIS A064152
101 = P13	Les cent une partitions du nombre 13.

Multiplication, division, diviseurs

101 = 1 x 101	Premier. Le plus petit à trois chiffres. Le seul premier en 100..001. Le seul premier en 1010 …1. Le troisième premier (après 2 et 11) dont la somme des chiffres est 2. Sans doute le plus grand.
		Clé de divisibilité par 101. Constituer des blocs de 2 chiffres. les additionner et soustraire alternativement. Le résultat doit être divisible par 101. Autre possibilité équivalente Ajouter les blocs de quatre chiffres. S'ils sont de la forme ABAB ou A0A, le nombre est divisible par 101. 1 + 2423 = 2424 => divisible par 101.
101 => 101, 103, 107, 109, 131, 151, 181, 191, 401, 601, 701		Le nombre 101 engendre onze nombres premiers en modifiant un de ses deux chiffres. Suivant 107 avec 13 cas.
9 999 = 3² × 11 × 101		Facteur de ce 9-repdigit.

Avec les puissances

101 = 1² + 10² = 1² + 6² + 8² = 2² + 4² + 9² = 4² + 6² + 7²	Sommes de carrés. Seules à deux et trois termes. Autres sommes de carrés >>>
101 = 10² + 1² 10 100 = 10² + 100² 1 233 = 12² + 33²	Motif singulier par concaténation. Le plus petit. Autres exemples. Autres sommes de carrés >>>
101 = 51² – 50² = 51 + 50	Motif valable pour tout nombre impair.
101 = 5 (5² – 5) + 1	Nombre décagonal centré.
101 = 1^3 + 1^3 + 2^3 + 3^3 + 4^3	Somme de cubes.

En puissance

101^3 = 1030301 = 100 x 101 x 102 + 101 = 1030200 + 101 = 1030301

Un cube est égal au produit du nombre par ses deux voisins plus le nombre >>>

	Les nombres en AB..BC au carré sont sources de motifs itératifs pour tout A et B avec C multiple de 3. Motifs semblable pour: 131, 161, 191, 201, 231, 261, 291, 301 … Débutant par: 100, 130, 160, 190, 200, 230, … Et finir par: 899, 909, 939, 969, 999.
101^2 = 10201 101^3 = 1030301 101^4 = 104060401	Puissances palindromes. Les puissances supérieures ne sont pas palindromes.
101^2 = 1 02 01 101^3 = 1 03 03 01 101^4 = 1 04 06 04 01 101^5 = 1 05 10 10 05 01 101^6 = 1 06 15 20 15 06 01 101^7 = 1 07 21 35 35 21 07 01 101^8 = 1 08 28 56 70 56 28 08 01	Manière simple et générale pour obtenir les premières lignes du triangle de Pascal. Prendre 1001 pour prolonger, en laissant la place aux nombres de trois chiffres de s'exprimer correctement. Voir Répétition de motifs / Nombre 111
101², 102², 103²	Motifs avec permutation des chiffres sur trois carrés de nombres consécutifs. >>>

101² = 1 02 01	= (100 + 1)² = 10 000 + 200 + 01	Calcul mental des carrés d'un nombre à trois chiffres comportant un zéro central. Procédé: Concaténation successive: du carré des dizaines, du double produit dizaine par unité, et du carré des unités, en tenant compte des retenues.
102² = 1 04 04	= (100 + 2)² = 10 000 + 400 + 04
108² = 1 16 64	= (100 + 8)² = 10 000 + 1 600 + 64
109² = 1 18 81	= (100 + 9)² = 10 000 + 1 800 + 81

cdu^101 = … cdu pour u = 1, 3, 7 ou 9

La puissance 101 conserve ses trois derniers chiffres selon la valeur des unités.

Dénombrement, jeux et curiosités

Jeu du quatre 4. Avec la notation anglaise: .4 = 0,4

Autour du nombre

123456789112233445566778899101	Les premiers palindromes concaténés jusqu’à 101 forment le plus grand nombre premier de la sorte jusqu'à 1 000 000 (et plus ?).
101 10101 1010101 ….	Suite alternée de 1 et 0. Seul 101 est premier.
Si x + y = 101 et x – y = A Alors x² – y² = AA	Exemple: x = 75 et y = 101 – 75 = 26 A = 75 – 26 = 49 75² – 26² = 49 49 Suite en x² - y²

Décimales

100 101	= 0,9900 9900 9900 9900 …	Nombre périodique. Le seul de longueur 4. 101 est un nombre premier unique. Nombre objet de motifs esthétiques.
Toutes les fractions avec 101 au dénominateur possèdent 4 décimales répétitives en 25 suites permutées. Notez que 4x25 = 100 = 101 – 1. Aussi, chaque suite est composées de chiffres reconstituant les multiples de 9.

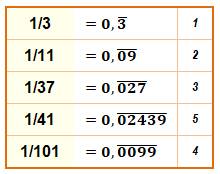
Fractions avec petites périodes

Identité détaillée

Voir Diviseurs, Quantité, Somme, Fonctions arithmétiques

Numération: base, [chiffres]			Repdigit (Brésilien)
101 2, [1, 1, 0, 0, 1, 0, 1] 3, [1, 0, 2, 0, 2] 4, [1, 2, 1, 1] 5, [4, 0, 1] 6, [2, 4, 5] 7, [2, 0, 3] 8, [1, 4, 5] 9, [1, 2, 2] 10, [1, 0, 1] 11, [9, 2]	12, [8, 5] 13, [7, 10] 14, [7, 3] 15, [6, 11] 16, [6, 5] 17, [5, 16] 18, [5, 11] 19, [5, 6] 20, [5, 1] 21, [4, 17]	22, [4, 13] 23, [4, 9] 24, [4, 5] 25, [4, 1] 26, [3, 23] 27, [3, 20] 28, [3, 17] 29, [3, 14] 30, [3, 11] 60, [1, 41]	Aucun

Voir Bases / Brésiliens

Suite	Autres pages sur ce nombre Nombre 102 Autres nombres 100 avec chiffres – Jeux
Voir	Nombres par leur nom Empreinte des nombres DicoNombre Junior Historique de ce site et Références Maitres en nombres
Cette page	http://villemin.gerard.free.fr/NombDico/N100a500/Nb101.htm