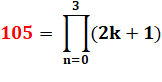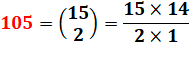|
Édition du: 02/05/2025 |
|
Dictionnaire des Nombres |
|||
|
1 / 10 / 50 / 60
/ 75 / 80
/ 81 / 82
/ 83 / 84
/ 85 / 86
/ 87 / 88
/ 89 / 90
/ 91 / 92
/ 93 / 94
/ 95 / 96
/ 97 / 98
/ 99 / 100 / 101 / 102 / 103
/ 104 |
105 |
106 / 107 / 108
/ 109 / 110 / 111 / 112 / 113
/ 114 / 115 / 120 / 130 / 140 / 150
/ 200 / 250 / 300 / 400 / 500 / 1000
/ Autres |
|
![]()
|
|
|
|
|
Suite en propriétés
arithmétiques |
|
|
|
105
+ 501 = 606 |
|
|
10510 = 12214
= 1518 = 7714 |
|
|
105 / 15 = 7 |
|
|
105 = 7 x 15 501 – (5 – 1) = 497 = 7 x 71 |
|
Addition et soustraction
|
105 = 1 + 2 + … + 13
+ 14
= (14 x 15) / 2 |
|
|
105 + 171 = 276 171 – 105 = 66 |
|
|
105 = 1 + 2 + … + 14 = 6 + 5 + … + 15 = 12
+ 13 + … + 18 = 15 + 16 + … + 20 = 19 + 20 + … + 23 = 34 + 35 + 3 6 = 52 + 53 |
|
|
105 = 15 + 16 + … + 20 = 21 x 5
= 15 + 14 + … + 6 =
5 x 21 |
|
Multiplication, division, diviseurs
|
105 = 3 x 5 x 7 = 7!! = 7# / 2 |
|
|
105 = 3 x 5 x 7 |
Voir Magie |
|
1 x 1 + 2 = 3 1 x 3 + 2 = 5 1 x 5 + 2 = 7 |
|
|
105
= 7!! = 7 x 5 x 3 x 1 |
|
|
105 = 15 x 7 108 = 18 x 6 121 = 11 x 11 132 = 12 x 11 … 891 = 81 x 11 |
Le
plus petit et les suivants. …
Le
plus grand à trois chiffres. |
|
Facteurs(105):
3, 5, 7 |
|
|
|
|
|
PGCD(105,
2k+1 < 105) = 1 |
|
|
105 – 2k
avec k de 1 à 6 => 103, 101, 97, 89, 73, 41 |
On
ne connait que 6 tels nombres: 7, 15, 21, 45, 75 et 105 |
Avec les puissances
|
105 = 1² + 2² + 10²
= 4² + 5² + 8² |
|
|
105² =
145² – 100² 11 025 = 21 025 – 10 000 |
|
||
|
|
Le
nombre 96 l'est également, mais il est pair. Avec
cinq différences: 144, 192, 225 … |
||
|
2105
= 40564819207303340847894 |
Liste: 105, 136, 137, 237, 268, 275,
336, 397, 409, 418, 423, 426, 456, 457, 486,
… Voir 125 Pour n², on trouve la première suite
pannumérique pour 32 043. Pour n3,
c'est 2326. |
||
Dénombrement, jeux et curiosités
|
105 |
|
|
|
|
|
|
|
|
|
|
|
105 = ½ ( 10 x 5² – 8
x 5) |
|
|
|
105 |
|
|
|
|
|
|
Autour du nombre
|
… 87, 93, 99, 105 … |
|
|
101 103 105 107 109 |
|
|
1 = 1/3 + 1/5 + 1/7 + 1/9 + 1/11 +
1/33 + 1/35 + 1/45 + 1/55 + 1/77 + 1/105 |
|
|
105 – 2n pour n =
{1, 2, 3, 4, 5, 6} = {103, 101, 97, 89, 73, 41} |
|
![]()
|
|
Voir Diviseurs, Quantité, Somme, Fonctions arithmétiques
|
Numération: base, [chiffres] |
Repdigit (Brésilien) |
||
|
105 2,
[1, 1, 0, 1, 0, 0, 1] 3,
[1, 0, 2, 2, 0] 4, [1, 2, 2, 1] 5,
[4, 1, 0] 6,
[2, 5, 3] 7, [2, 1, 0] 8, [1, 5, 1] 9,
[1, 2, 6] 10,
[1, 0, 5] 11,
[9, 6] |
12, [8, 9] 13,
[8, 1] 14, [7, 7] 15,
[7, 0] 16,
[6, 9] 17,
[6, 3] 18,
[5, 15] 19,
[5, 10] 20, [5, 5] 21,
[5, 0] |
22,
[4, 17] 23,
[4, 13] 24,
[4, 9] 25,
[4, 5] 26,
[4, 1] 27,
[3, 24] 28,
[3, 21] 29,
[3, 18] 30,
[3, 15] 60,
[1, 45] |
14,
[7, 7] 20,
[5, 5] 34,
[3, 3] 104,
[1, 1] |
Voir Bases / Brésiliens
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()