Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 30/04/2025 M'écrire Brèves de Maths

DicoNombre Débutant Glossaire Types de nombres Nombres géométriques Nom des nombres Écriture des nombres Table des facteurs Nombres et anglais Langues	Dictionnaire des Nombres
	1 / 10 / 50 / 70 / 80 / 90 / 100 / 105 / 110 / 111 / 112 / 113 / 114 / 115 / 116 / 117 / 118 / 119 / 120 / 121 / 122 / 123 / 124 / 125 / 126	127	128 / 129 / 130 / 131 / 132 / 133 / 134 / 135 / 140 / 150 / 160 / 170 / 180 / 190 / 200 / 250 / 300 / 400 / 500 / 1000 / Autres

Cent-vingt-sept

One hundred (and) twenty-seven

Orthographe / Langues

Facteurs
Diviseurs	1, 127
Binaire	111 1111
Romain	CXXVII

Suite en propriétés arithmétiques

Chanceux d'Ulam

Composé

Congruent

Cunningham (2⁷ – 1)

Déficient

Friedman

Impair

Motzkin

Obstiné

Panconsommable

Premier

Premier bon

Premier brésilien

Premier cubain

Premier de Chen,

Premier de Mersenne

Premier de Motzkin

Premier de Ramanujan

Premier de Woodall

Premier fort

Premier régulier

Géométrique

Hexagonal centré (7^e)

21 – gonal centré

Multimédia	127 chiffres Message déchiffré après 17 ans de progrès.	>>>
Social	Position 127: La position de l'ado vautré sur le canapé est la position la plus proche de la position gravité zéro calculée par la Nasa pour les sièges des astronautes, avec un angle de 127° entre le dossier et l'assise (en fait entre 121° et 135° entre le buste et les hanches). C'est aussi l'angle des sièges de la classe affaires d'Air France. Fauteuil zéro gravité: Cette posture permet l’alignement du cœur, des jambes et du dos afin de provoquer une relaxation totale. Notre corps ressent environ sept fois moins de gravité qu’une position classique, l’équivalent d’être dans l’eau.

Chiffres et numération

127 + 721 = 848 127 + 7x2x1 = 141	Devient palindrome en lui ajoutant son retourné et aussi avec le produit des chiffres.
127 = (1x6x1x2x9) + (1+6+1+2+9)	Nombre somme-produit.
127 = 111 11112	Rep-unit en binaire. Connu par les informaticiens pour être le plus grand nombre avec signe codé sur un octet (8 bits).
127 = – 1 + 2^7 111 111 = (1 + 1)^111 – 1 x 1	Nombre de Fiedman (égal à une opération avec ses chiffres). Il l'est également en base 2.

Représentations du nombre 127 en double-base

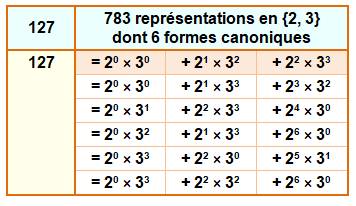
Voir Double-base

Addition et soustraction

127 = 3 + 5 + 7 + 11 + 13 + 17 + 19 + 23 + 29	Somme des neufs premiers nombres premiers impairs. Le plus petit premier avec cette somme commençant par 3, 5 …
127 = 1 + 3 + 4 + 7 + 6 + 12 + 8 + 15 + 13 + 18 + 12 + 28	Somme de la somme des diviseurs des nombres jusqu'à 12.
127 = 1! + 3! + 5!	Somme de factorielles.
127 = 1 + 3 + 5 + 8 + 21 + 34 + 55 127 = 1 + 3 + 13 + 21 + 34 + 55 127 = 1 + 3 + 5 + 8 + 21 + 89 127 = 1 + 3 + 13 + 21 + 89 127 = 1 + 3 + 34 + 89		Recherche de la partition de Zeckendorf (exemple). Il existe cinq partitions de 137 en somme de nombres de Fibonacci. Pour la quatre premières, on note des nombres de Fibonacci successifs (jaune). Seule la dernière monte des nombres de Fibonacci isolés, c'est la partition de Zeckendorf, la seule, comme le prévoit le théorème.

Multiplication, division, diviseurs

127 = 6 x 21 + 1	Nombre hexagonal centré.
127 = 2 x 8² – 1	Nombre premier de Woodall d'ordre 8.
127 est premier 129 = 3 x 43, semi premier	Nombre premier de Chen. Le plus petit nombre premier à trois chiffres dont tous les chiffres vont croissants.
... [12, 211], [14, 127], [16, 1847], …	Plus petits nombres premiers avec écart croissant par rapport au premier précédent.
127 – 113 = 14 307 – 293 = 14 331 – 317 = 14 787 – 773 = 14	Premier cas avec un tel intervalle entre premiers successifs.
113, 114, …126, 127	Première rencontre de 13 nombres composés consécutifs (de 114 à 126).
127 (2^7n – 1)	Propriété générale des nombres de Mersenne composés. (Barre verticale = divise)
	Somme des diviseurs en puissance 7. Précédent: 93
1, 2, 3, 5, 11, 31, 127, 709, 5381, 52711, 648391, …	Suite de premiers telle que le suivant est le nombre premier du rang du précédent. Ainsi 127 est le 31^e nombre premier. OEIS A007097

Avec les puissances

127 = 2^7 – 1 = M7 M = 2 ^127 – 1 = 1,7… 10^38 2^6 x (2^7 – 1) = 8 128	4^e Nombre de Mersenne premier. Repunit en binaire >>> Exposant d'un nombre de Mersenne premier. Comme tout nombre de Mersenne, 127 permet de calculer son conjugué parfait.
127 = MM3 = M7 = 2^2x3 + 1 – 1	Nombre double de Mersenne. Nombre triple de Mersenne, car 3 est aussi nombre de Mersenne.

127 = 2^0 + 2^1 + 2^2 + 2^3 + 2^4 + 2^5 + 2^6 = 2^7 – 1	Somme puissances de 2. Cette égalité est une propriété générale.
127 = 2² + 5² + 7² + 7²	Somme de carrés de nombres premiers.
127 = 3² + 3² + 3² + 10²	Autre somme de carrés.
127 = 1^3 + 1^3 + 5^3 = 1^3 + 2^3 + 3^3 + 3^3 + 4^3	Somme de cubes.
127 = 7^3 – 6^3 = 343 – 216	Nombre binomial. Premier, différence de deux cubes successifs; tous de la forme 6k + 1. Parfois écrit sous la forme: et baptisés premier-cubes.

En puissance

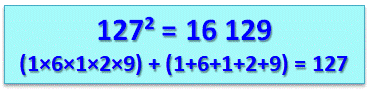
127² = 16 129 127 = 1x6x1x2x9x + (1+6+1+2+9) = 108 + 19 = 127

Plus petit nombre n tel que le produit des chiffres du carré augmenté de leur somme soit égal à n. Unique ? Aucune solution avec les cubes ?

Dénombrement, jeux et curiosités

Jeu du quatre 4.

Décimales

Toutes les fractions avec 127 au dénominateur possèdent 42 décimales répétitives en trois suites permutées.

Fractions en 127

Valeurs citées par Robert Mufano

Identité détaillée

Voir Diviseurs, Quantité, Somme, Fonctions arithmétiques

Numération: base, [chiffres]			Repdigit (Brésilien)
127 2, [1, 1, 1, 1, 1, 1, 1] 3, [1, 1, 2, 0, 1] 4, [1, 3, 3, 3] 5, [1, 0, 0, 2] 6, [3, 3, 1] 7, [2, 4, 1] 8, [1, 7, 7] 9, [1, 5, 1] 10, [1, 2, 7] 11, [1, 0, 6]	12, [10, 7] 13, [9, 10] 14, [9, 1] 15, [8, 7] 16, [7, 15] 17, [7, 8] 18, [7, 1] 19, [6, 13] 20, [6, 7] 21, [6, 1]	22, [5, 17] 23, [5, 12] 24, [5, 7] 25, [5, 2] 26, [4, 23] 27, [4, 19] 28, [4, 15] 29, [4, 11] 30, [4, 7] 60, [2, 7]	2, [1, 1, 1, 1, 1, 1, 1] 126, [1, 1]

Voir Bases / Brésiliens

Suite	Nombre 128 Autres nombres
Voir	Nombres par leur nom Empreinte des nombres DicoNombre Junior Historique de ce site et Références Maitres en nombres
Cette page	http://villemin.gerard.free.fr/NombDico/N100a500/Nb127.htm