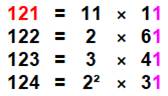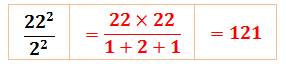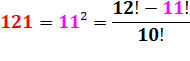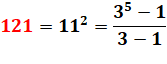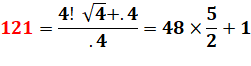dictionnaire des nombres – cent vingt et un

Édition du: 06/11/2024

M'écrire

Brèves de Maths

DicoNombre

Débutant

Glossaire

Types de nombres

Nombres géométriques

Nom des nombres

Écriture des nombres

Table des facteurs

Nombres et anglais

Langues

Dictionnaire des Nombres

1 / 10 / 50 / 70 / 80 / 90 / 100 / 101 / 102 / 103 / 104 / 105 / 106 / 107 / 108 / 109 / 110 / 111 / 112 / 113 / 114 / 115 / 116 / 117 / 118 / 119 / 120

121

122 / 123 / 124 / 125 / 126 / 127 / 128 / 129 / 130 / 131 / 132 / 133 / 134 / 135 / 140 / 150 / 200 / 250 / 300 / 400 / 500 / 1000 / Autres

Cent-vingt-et-un

One hundred (and) twenty-one

Orthographe / Langues

Facteurs
Diviseurs	1, 11, 121
Binaire	111 1001
Romain	CXXI

Suite en propriétés arithmétiques

Auto-nombre

Brésilien

Brillant

Composé

Déficient

Dihédral

Docile (amenable)

Fourchette ou gapful

Friedman

Impair

Palindrome

Semi-premier

Smith

Tarte (15 coupes)

Touchable (hautement)

Géométrique

Carré

Dodécagonal centré

Hexagonal concentrique (9^e)

Icosagonal centré

Nombre étoilé

Octogonal centré (6^e)

121 = 11 11 – Multiplication posée

Jeux

Le damier chinois possède 121 alvéoles (nombre étoilé).

6 x 10

+ 2 x (5 + 6 + 7 + 8)

+ 9

= 121

>>>

Géographie

121 nombres de villes aux États-Unis portant le nom de

Washington, y compris la capitale fédérale.

>>>

Chimie

121 Numéro atomique de l'unbiunium non découvert.

>>>

Chiffres et numération

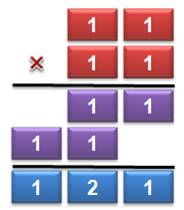
1, 2, 1	Ses chiffres sont la deuxième ligne du triangle de Pascal.
1 + 2 + 1 = 4 (1 + 1) + (1 + 1) = 4	Nombre de Smith. Somme des chiffres = celle des facteurs.
121 = 11² (2) = (1 + 1)	Nombre tel que la somme des chiffres pairs est égale à celle des impairs. Plus petit carré. Liste: [121, 11], [10201, 101], [12100, 110], [26569, 163], [29584, 172], [30625, 175], [34225, 185], [54289, 233], [69696, 264], [77284, 278], [185761, 431], [231361, 481], [294849, 543], [398161, 631], [403225, 635], [469225, 685], … Non répertorié dans le DicoNombre.
121 = 11²	Anagrammes numériques. Nombre de Friedman. Nombre Demlo (carré d'un repunit).
121 = 11 x 11 = 121 1331 = 11 x 11 x 11 = 1331 14641 = 11 x 11 x 11 x 11 = 14641			Relations palindromes. Voir Nombre 11
40 = 1 111₃ 121 = 11 111₃ 364 = 111 111₃		Repunit en base 3.
121 = 11111₃ = 232₇ = 171₈		Palindrome aussi palindrome en bases 3, 7 et 8. Le seul autre connu avec des bases <10 est 373.

Addition et soustraction

121 = 11² = 6 + 7 +…+ 16	Somme d'entiers consécutifs = carré. >>>
= 22 + 99 = 33 + 88 = 44 + 77 = 55 + 66	Somme de deux repdigits. Seuls quatre nombres partagent cette propriété.
121 = 6 + 7 + … + 16 = 60 + 61	Deux seules sommes de nombres consécutifs >>>
121 = 37 + 41 + 43	Somme de premiers consécutifs.
121 = T₁₀ + T₁₁ = n² + 2n + 1 avec n = 10	Somme de nombres triangulaires consécutifs.
121 = 29 + 92 = 11 x 11 = 38 + 83 = 47 + 74 = 56 + 65	Nombre NRC: nombre + retourné = carré
121 …	Tous les nombres à partir de 121 sont somme de premiers distincts de la forme 4n + 1.
121 = 1 + 3 + 5 +…+ 21	Le carré de n est la somme des n premiers impairs. Avec une coquetterie.
121 100a + 10b + c + a + b + c	Nombre Auto-nombre.
121 = 38 + 83	Somme palindromique.
121 = 5! + 1 = 11²	Un des trois seuls cas. Voir Problème de Brocard.

Multiplication et division

121 / 11 = 11

Nombre fourchette.

121 = 8 x 15 +1

Nombre Octogonal centré (6^e).

121 = (6! + 3! ) / 3!

Division avec factorielles.

Plus petite suite de quatre nombres dont le plus grand facteur se termine par 1.

121 = 1 + 2 x 3 x 4 x 5 = 5! + 1

Motif avec nombres consécutifs.

121 mod n = 1

pour n = {2, 3,…, 6}

Divisé par 2, 3, 4, 5 ou 6 ce nombre donne un reste de 1. La quantité de diviseurs de 120 explique cette propriété.

121

[243, 791, 1199, 1391, 1751, 1919, 2231, 2759, 3071, 3239, 3431, 3551, 3599]

Nombre hautement touchable.

Le nombre 121 est la somme des diviseurs propres de ces 13 nombres (somme aliquote).

Plus petite valeur pour 13 sommes.

Un motif qui donne envie de formuler une conjecture …

Tous les nombres de ce tableau – nombre en 1 sauf le deuxième chiffre qui est 2 – sont composés.

Est-ce que cette suite continue sans nombre premier ?

Non ! Mais, il faut atteindre un tel nombre en 1211… avec 137 fois "1" (138 chiffres) pour trouver un nombre premier.

Avec d'autres chiffres que le "2" ?

1, 1, 11

2, 137, 12111…

3, 1, 13

4, 10, 14111111111

5, 2, 151

6, 4, 16111

7, 1, 17

8, 2, 181

9, 1, 19

Le plus petit nombre premier de la forme 1k111…

Sauf pour 2, cette forme est vite un nombre premier.

Par exemple avec k = 5, le nombre avec deux "1" (151) est premier.

Voir Brève 867

Puissance

121 = 11² et 1 + 2 + 1 = 4 = 2² 121 = 22² / (1 + 2 + 1)	Plus petit carré palindrome. Carré palindrome d'un palindrome. Nombre doublement carré. Suite ascendante et descendante (propriété générale).
121 x (1 + 2 + 1) = 22² 12321 x (1 + 2 + 3 + 2 + 1) = 333² …	Ce motif continue jusqu'à obtenir un 9 central. Voir explication de cette propriété.
121	Plus petit carré qui est un nombre étoilé.
121 x (1 + 2 + 1) = 22² 11² x 2² = 22²	Deux écritures pour le même résultat remarquable. Voir Généralisation
121 = 11² = 11111₃ = 1 + 3 + 9 + 27 + 81 = (3⁵ – 1) / 2 = 242 / 2	Un des trois brésiliens connus en tant que puissance. Seul cas avec un nombre premier (11). De ce fait, 121 est la somme des puissances successives de 3.
121 = 11²	Nombre de Friedman. Égal à expression utilisant ses propres chiffres. Voir joli calcul en pyramide.
121 = 61² – 60² = 11² = 11² x 1²	Nombre complètement carré.
121, 660, 671 121, 7 320, 7 321	Triplets de Pythagore.
121 = 11² = 7² + 2 x 6²	Autour des triplets de Pythagore.
	Un des trois tels motifs.
	Carré = cette relation entre factorielles successives.
121 + 4 = 5³ 4 + 4 = 2³	Seul carré, avec 4, qui devient un cube en ajoutant 4. Conjecture de Fermat.
	Seuls trois motifs de ce genre sont connus: 121, 343 et 400.
121 = 2² + 6² + 9² = 6² + 6² + 7² = 1² + 2² + 4² + 10² = 1² + 2² + 4² + 6² + 8²	Sommes de carrés.
121 = 3⁰ + 3¹ + 3² + 3³ + 3⁴ = 1 + 3 + 9 + 27 + 81 n² = p⁰ + p¹ + p² + p³ + p⁴	Somme de puissances de 3 successives. C'est le seul carré connu formé avec une telle somme d'un nombre premier porté à cinq puissances successives.

En puissance

La racine de ces nombres "en toit" est le repunit comportant autant de 1 que l'indique le chiffre central.

121² = 14641

Palindrome dont le carré est palindrome.

Puissance palindrome.

Pas vraie pour les puissances supérieures.

Jeux

121	De nombreux nombres donnent 121 en palindrome retard.
	Le nombre 121 se prête à ces formes palindromiques. Le motif se prolonge indéfiniment avec les repdigits en 9. Avec 98, 97 … on met en évidence des sommes retournées.
		Jeu du quatre 4. Avec la notation anglaise: .4 = 0,4 = 2/5

Identité détaillée

Voir Diviseurs, Quantité, Somme, Fonctions arithmétiques

Numération: base, [chiffres]

Repdigit (Brésilien)

121

2, [1, 1, 1, 1, 0, 0, 1]

3, [1, 1, 1, 1, 1]

4, [1, 3, 2, 1]

5, [4, 4, 1]

6, [3, 2, 1]

7, [2, 3, 2]

8, [1, 7, 1]

9, [1, 4, 4]

10, [1, 2, 1]

11, [1, 0, 0]

12, [10, 1]

13, [9, 4]

14, [8, 9]

15, [8, 1]

16, [7, 9]

17, [7, 2]

18, [6, 13]

19, [6, 7]

20, [6, 1]

21, [5, 16]

22, [5, 11]

23, [5, 6]

24, [5, 1]

25, [4, 21]

26, [4, 17]

27, [4, 13]

28, [4, 9]

29, [4, 5]

30, [4, 1]

60, [2, 1]

3, [1, 1, 1, 1, 1]

120, [1, 1]

Voir Bases / Brésiliens

Retour	Nombre 120
Suite	Nombre 122 Autres nombres
Voir	Nombres par leur nom Empreinte des nombres DicoNombre Junior Historique de ce site et Références Maitres en nombres
Site	Références Internet
Cette page	http://villemin.gerard.free.fr/NombDico/N100a500/Nb121.htm