Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 29/07/2022 M'écrire Brèves de Maths

INDEX Triangle Géométrie	Droites dans le triangle
	Droites et points	Droite d'Euler	Droite de Simson
	Th. de Desargues

Faites un double-clic pour un retour en haut de page

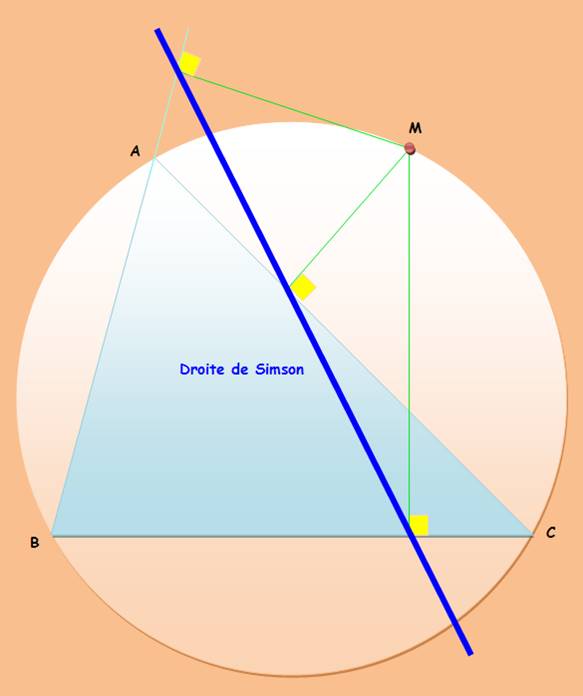
Droite de Simson Droite particulière dans le triangle.
	Sommaire de cette page >>> Droite de Wallace-Simson >>> Démonstration >>> Historique	Débutants Triangle Glossaire Triangle

DROITE de WALLACE-SIMSON

Un point M sur le cercle circonscrit à un triangle quelconque. Les perpendiculaires aux trois côtés; leurs pieds sont alignés sur la droite de Simson. Réciproquement Les pieds des perpendiculaires abaissées d'un point sur les côtés d'un triangle sont alignés si, et seulement si, ce point appartient au cercle circonscrit au triangle. Lorsque le point M se déplace sur le cercle, la droite de Simson enveloppe un deltoïde de Steiner. Cette enveloppe est indépendante de la forme du triangle initial, à une similitude près. Deltoïde: courbe décrite par un point d'un cercle roulant sans glisser à l'intérieur d'un cercle triple. Généralisation Le théorème reste valable si on remplace l'angle droit des pieds des perpendiculaires par un angle quelconque par rapport à chacun des côtés.

Démonstration
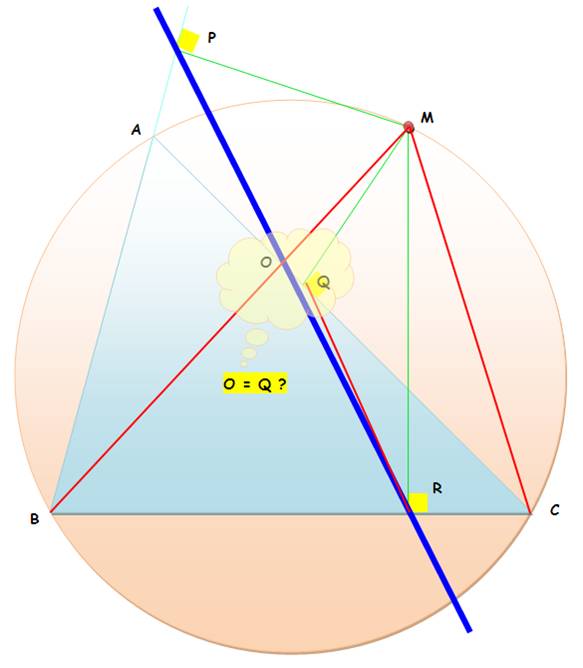
Hypothèses Un triangle ABC et son cercle circonscrit; un point M sur ce cercle. Les trois perpendiculaires en M aux côtés du triangle: P, Q et R. La droite PR coupe AB en O. Ce qu'il faut démontrer Les points Q et O sont confondus Théorèmes invoqués Dans un cercle, les angles inscrits interceptant un même arc sont égaux. Deux triangles rectangles ayant leur hypoténuse en commun forment un quadrilatère inscriptible. l'hypoténuse est un diamètre du cercle.	Démonstration Quadrilatère BPMR, avec deux angles droits est inscrit dans un cercle: PBM = PRM ABM = ORM Quadrilatère MRCQ, avec deux angles droits est inscrit dans un cercle: QRM = ACM Quadrilatère ABCM, par hypothèse: ABM = ACM En rapprochant ces égalités: ORM = QRM Avec le même angle, sachant que Q comme O sont sur AC, les points O et Q sont confondus. Les points P, Q et R sont alignés.

Historique

Robert Simson (1687-1768) – Mathématicien anglais.

Le théorème a été attribué à Simson. Aucune trace évidente de son travail sur ce sujet.

On connaît Simson pour être le premier à avoir traduit les Éléments d'Euclide en anglais. Il a étudié la suite de Fibonacci et son rapport au nombre d'or: F_n+1 / F_n tend vers le nombre d'or.

William Wallace (1768-1843) – Mathématicien écossais.

Le premier écrit connu sur ce théorème date de 1799 et, il est dû à W. Wallace.

Voir Contemporains en 1600 et en 1700

Voir	Triangle – Index Triangle – Glossaire Éléments de géométrie Triangle – Débutants, novices DicoMot DicoNombre Les trois perpendiculaires