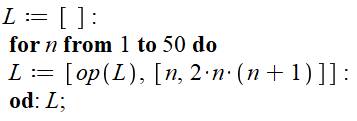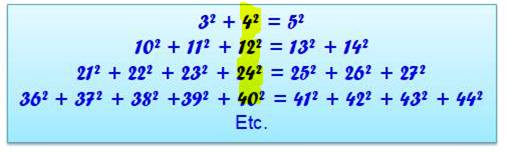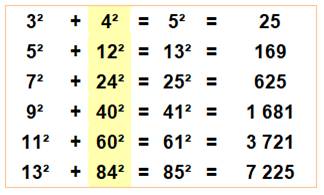|
Édition du: 09/03/2024 |
|
INDEX |
QUADRILATÈRES – Compter |
||
|
|
|||
![]()
|
Quantité de segments dans une grille Nombres quadrillages
Dessinez un quadrillage et
amusez-vous à compter les segments élémentaires. La formule donnant la quantité
de segments est extraordinairement simple! Une série de nombres qui
côtoie les nombres triangulaires, les
nombres carrés centrés, les triplets de Pythagore ou encore les belles
égalités de comme de carrés consécutifs. |
||
|
|
Sommaire de cette page >>> En bref >>> Dénombrement >>> Liste >>> Égalité de sommes de
carrés consécutifs >>> Triplets de
Pythagore |
Débutants Glossaire |
|
12 = 2 (2 x 3) = 4 T2 = CC2 –
1 = 2² + 3² – 1 5² + 12² = 13² 10² + 11² + 12² = 13² + 14² |
Ensemble,
ces propriétés sont communes à toute une série de nombres: 4, 12, 24, 40 … |
Voir Nombre 12 –
DicoNombre
|
|
||
|
Observations Le carré
comporte, bien évidemment quatre côtés. Avec une
grille de 2 x 2 carrés, on compte 12 segments:
Avec une grille
de 3 x 3 carrés, on compte 24 segments:
On
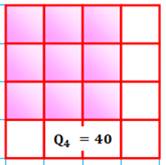
constate une logique de comptage. Appliquons la à la grille 4 x 4
Conclusion La
formule générale est indiquée sur l'illustration. On y reconnait le produit
de deux nombres consécutifs, d'où la formulation avec les nombres triangulaires
Tn. |
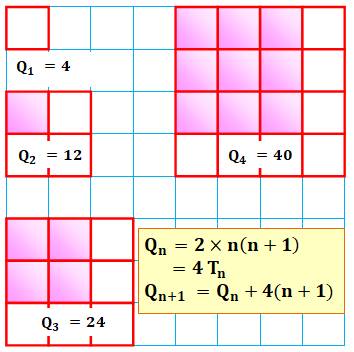
Quadrillage de n = 1 à n = 4
Théorèmes La quantité de segments pour une grille n On passe de la grille n à la grille n + 1 en ajoutant quatre fois n +
1. |
|
|
|
||
|
Formules Qn
= 2n (n + 1) Qn+1
= Qn + 4 (n + 1) Programmation (Maple)
Rapprochement Ajoutez 1 à cette liste, et
vous obtenez la liste des nombres
carrés centrés qui est aussi la somme de deux carrés consécutifs: CCn = 2n (n + 1) + 1 = (n + 1)² + n² |
Liste des 100 premiers 4, 12, 24, 40, 60, 84, 112, 144, 180, 220, 264, 312, 364, 420, 480, 544,
612, 684, 760, 840, 924, 1012, 1104, 1200, 1300, 1404, 1512, 1624, 1740,
1860, 1984, 2112, 2244, 2380, 2520, 2664, 2812, 2964, 3120, 3280, 3444, 3612,
3784, 3960, 4140, 4324, 4512, 4704, 4900, 5100, 5304, 5512, 5724, 5940, 6160,
6384, 6612, 6844, 7080, 7320, 7564, 7812, 8064, 8320, 8580, 8844, 9112, 9384,
9660, 9940, 10224, 10512, 10804, 11100, 11400, 11704, 12012, 12324, 12640,
12960, 13284, 13612, 13944, 14280, 14620, 14964, 15312, 15664, 16020, 16380,
16744, 17112, 17484, 17860, 18240, 18624, 19012, 19404, 19800, 20200, … Liste avec rang
|
|
Voir Programmation – Index
|
|
||
|
Le
nombre qui précède le signe égal à Q: Qn = 2n (n + 1) = 4Tn |
|
|
Voir Somme de
carrés consécutifs = somme de carrés consécutifs
|
|
||
|
Les Qn
représentent également les termes des triplets
de Pythagore jumeaux par l'hypoténuse tels que: a² + b² = (b +
1)² b est un nombre quadrillage, et b + 1 est
un nombre carré centré. |
|
|
Merci à
Jean-Louis Breuil pour l'idée de cette page
![]()
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
![]()