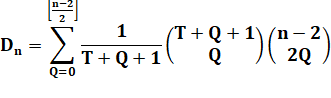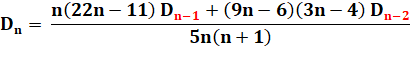Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 06/06/2025 M'écrire Brèves de Maths

INDEX Types de triangles Triangle Polygones	Polygones – Partages
	Diagonales dans les polygones	Régions externes
	Triangles dans les polygones	Régions et intersections
	Partage par les diagonales (Hexagone)	Dissection de l'heptagone

Faites un double-clic pour un retour en haut de page

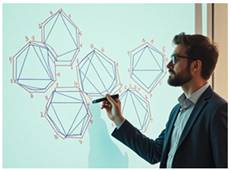
Dissection des polygones partagés par les diagonales Prenons l'hexagone et ses diagonales non-sécantes. Notre but est d'évaluer la quantité de partitions (ou partages) qui sont réalisables. Partage en triangles, carrés ou autres polygones. La quantité de partage en triangles est le travail des nombres de Catalan. Avec d'autres polygones, c'est le but des nombres Hyper-Catalan.
	Sommaire de cette page >>> Hexagone – Présentation >>> Hexagone – Les dissections >>> Hexagone – Bilan	Débutants Triangle Glossaire Triangle

Hexagone – Présentation		haut
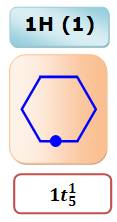
Dissection de l'hexagone On se propose de faire l'inventaire de toutes les possibilités de partages de l'hexagone par ses diagonales non-sécantes. Pour éviter de compter les cas de rotations et permutations, l'hexagone est maintenu dans sa position initiale repérée par un rond bleu. Hexagone par hexagone Il s'agit évidemment d'une dissection triviale. Elle ne comporte qu'un exemplaire. La forme utilisée pour la dissection est un hexagone, noté 5 (nombre de côtés – 1, convention utile pour d'autres applications).
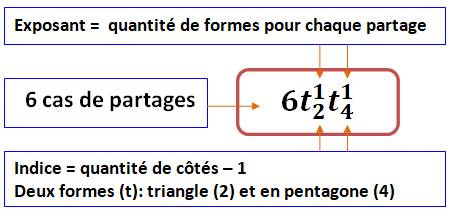
Principe de la numérotation

Hexagone – Les dissections		haut
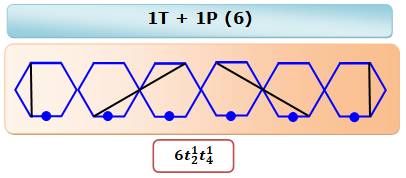
Dissection avec pentagones Une seule diagonale suffit. Avec le pentagone vient un triangle pour couvrir la totalité de l'hexagone. Naturellement, on identifie 6 cas de dissections.
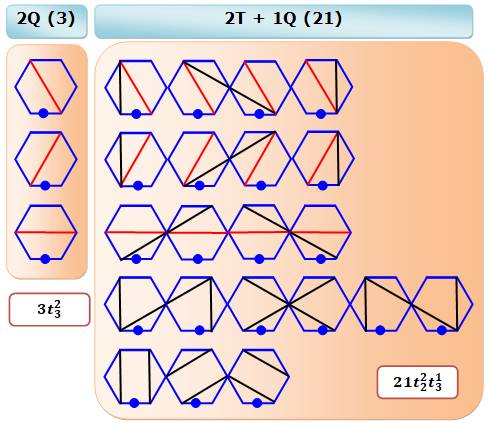
Dissection avec quadrilatères Deux possibilités: deux quadrilatères, ou un quadrilatère et deux triangles. Une présentation logique des cas permet de réaliser facilement le dénombrement: 3 cas pour deux quadrilatères et, 21 cas pour un quadrilatère et deux triangles.
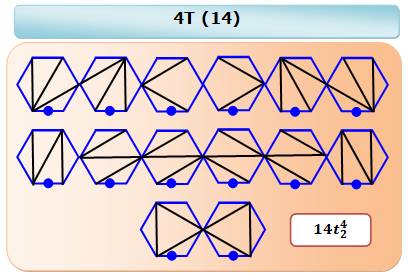
Dissection avec des triangles Ce cas est classique. En procédant logiquement, on trouve les 14 partitions de l'hexagone en triangles. Cette quantité est représentée par le quatrième nombre de Catalan

Hexagone – Bilan		haut
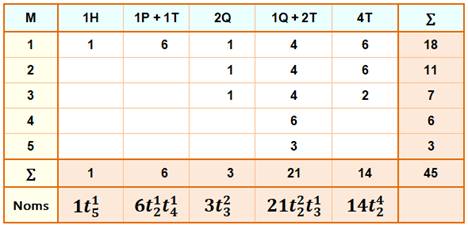
Dissection de l'hexagone Le tableau récapitule le décompte selon les cas de dissection. Il existe donc 45 possibilités de partage de l'hexagone par ses diagonales non-sécantes et cela selon tous les polygones possibles en partant du triangle et en allant à l'hexagone lui-même.

Compter les formes				haut
Dissection des polygones Un polygone à n côtés est triangulé avec n – 2 triangles. Exemple: 6 côtés pour l'hexagone et 4 triangles pour sa triangulation. T = N – 2 Tenir compte des quadrilatères revient à grouper deux triangles en un quadrilatère. Dit-autrement, un quadrilatère compte pour deux triangles. T + 2Q = N – 2		Formule de la dissection en T et Q
Exemple Décompte dans le cas de l'hexagone: 2Q => 3 2T + 1Q => 21 4T => 14 Total: 38	Liste: quantité de dissections des polygones en triangles et quadrilatères (à partir de 2) 1, 1, 3, 10, 38, 154, 654, 2871, 12925, 59345, 276835, 1308320, 6250832, 30142360, 146510216, 717061938, 3530808798, 17478955570, 86941210950, 434299921440, 2177832612120, 10959042823020, 55322023332420, 280080119609550, 1421744205767418, 7234759677699954, … OEIS A001002
Formule de récurrence
Programme Python Simple déroulement du calcul de la formule de récurrence. Décomposition de la formule avec A, B et C pour éviter toute erreur de parenthèses. Notez la commande de print du résultat q. But: imprimer 3 comme nombre entier et non 3.0 qui est le nombre décimal résultat du calcul.

Voir Programmation – Index

Haut de page (ou double-clic)

Retour	Régions et intersections
Suite	Compter les triangles dans les polygones Compter les triangles dans une figure quelconque Devinette avec deux triangles Dissection de l'heptagone Longueurs des diagonales Quantité d'intersections dans les polygones
Voir	Carré dans le triangle, construction astucieuse Dénombrement – Index DicoMot Géométrie – Index Heptagone et ses diagonales Jeux et puzzles – Index Nombres triangulaires Polygones – Index Triangle – Index
Sites
Cette page	http://villemin.gerard.free.fr/GeomLAV/Triangle/Particul/Partage.htm