NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 21/11/2024 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	TRIANGLES
Débutants Triangle	Propriétés – Curiosités				Glossaire Triangle
INDEX Types de triangles Triangle Dénombrement	Point Milieu	Droites et points	Pappus	Point et triangles
	Angles (180°)	Quantité de triangles	Torricelli	Triangles et triangles
	Triangulation	Quatre triangles	Heilbron	Carrés triangles
		Triangles de Kobon
	Triangles trois en cinq	Représentation	Brocard	Cercles et triangles
		Triangles dans les polygones		Démo fallacieuse
		Sommaire de cette page >>> Combien de triangles avec k droites

Triangles de Kobon

ou problème de Fujimura

Des droites sécantes qui forment des triangles: combien de triangles ?

Combien de triangles avec k droites		haut
Triangles de Kobon ou problème de Fujimura C'est le japonais Kobon Fujimura qui formule de problème : quel est le nombre maximal de triangles distincts pouvant être construits à l'aide d'un nombre donné de segments de droite ? Le problème fut popularisé par Martin Gardner en 1983. Solutions Facile au début : cinq droites, cinq triangles ; six droites, sept triangles. Il a été beaucoup plus difficile de montrer que sept droites pouvaient découper onze triangles. Il n'existe aucune formule donnant la quantité de triangles en fonction de la quantité de droites. 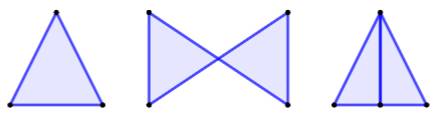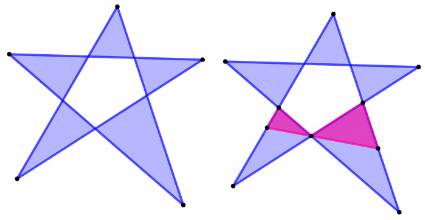Voir Références pour autre exemples	Trois droites – Un triangle & Quatre droites – Deux triangles Cinq droites – Cinq triangles & Six droites – Sept triangles Sept droites – Onze triangles
Valeurs connues Voir OEIS A006066

Anglais: How many disjoint triangles can you make out of n line segments?

Voir Brève 59-1164 (avec solution pour huit droites)

Suite	Quantité de triangles Triangle de Heilbronn Devinette avec deux triangles Compter les triangles dans les polygones
Voir	Carré dans le triangle, construction astucieuse Dénombrement – Index DicoMot Géométrie – Index Jeux et puzzles – Index Nombres triangulaires Polygones Triangle – Index
Sites	Triangle de Kobon – Wikipédia Kobon Triangles – Math Games Kobon Triangle – Wolfram MathWorld Roberts's triangle theorem – Wikipédia A list of problems in Plane Geometry with simple statement that remain unsolved – Felipe Prieto-Martınez
Cette page	http://villemin.gerard.free.fr/GeomLAV/Triangle/Particul/Kobon.htm