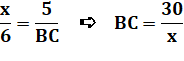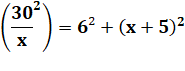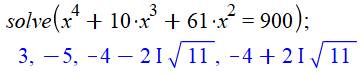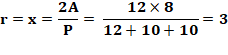Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 04/12/2024 M'écrire Brèves de Maths

INDEX Défis en géométrie Géométrie Jeux et énigmes	Énigmes en géométrie
	Quatre carrés	Tête géométrique	Carré et 2 Trg Équilatéraux
	Exercices 01	Escalier dans cercle	Rect et 2Trg Equilatéraux
	Triangles gigognes	Carrés dans cercle	Triangle dans le cercle
	Triangle et bissectrice		Triangle dans carré

Faites un double-clic pour un retour en haut de page

TRIANGLE et BISSECTRICE Une bissectrice dans le triangle rectangle. Mesures sur la découpe du carré.
	Sommaire de cette page >>> Bissectrice dans le triangle rectangle	Débutants Géométrie Glossaire Géométrie

DicoMot: Bissectrice / Angle bisector

Bissectrice dans le triangle rectangle		haut
Simple problème de géométrie, mais la solution nécessite la résolution d’une équation du quatrième degré.
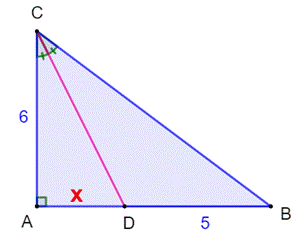
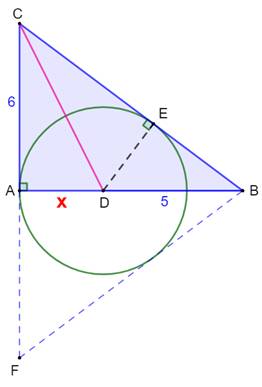
Construction Un triangle rectangle et la bissectrice d’un des angles non-droit. Un des côtés mesure 6 cm et la bissectrice découpe le côté opposé en deux segments de mesures x et 5 cm. Quelle est la valeur de x ? Première idée – Intuition S'agit-il d'un triangle rectangle dont les longueurs des côtés sont des nombres entiers ? En ce cas, pourquoi pas un triplet de Pythagore (6, 8, 10) multiple du triplet de base (3, 4, 5). En effet: 6² + 8² = 36 + 64 = 100 = 10² Alors x = 8 – 5 = 3.	Figure initiale
Recherche de démonstration La bissectrice découpe le côté AB en segments proportionnels aux côtés : Théorème de Pythagore dans ABC : Solution Avec cette équation du quatrième degré, on tente x = 1, 2 et 3. Une seule solution réelle positive. La solution est x = 3 cm.	Notez que: en dessinant le triangle symétrique, les points A et E sont sur le cercle inscrit au triangle BCF. Notez aussi que CA = CE (tangentes) Rayon du cercle connaissant le triangle :

Haut de page (ou double-clic)

Retour	Théorème de la bissectrice Exercices sur le triangle – Niveau lycée
Suite	Constructions élémentaires: triangle rectangle Résolution du triangle rectangle Doubler le triangle rectangle Quadrupler le triangle rectangle Triangles rectangles particuliers Types de triangles Triangle – Index
Voir	DicoMot Droite Égalités des triangles Enseignement – Collège Géométrie – Index Résolution du triangle quelconque Triangle de Pythagore
Cette page	http://villemin.gerard.free.fr/GeomLAV/Triangle/Exercice/TrianBis.htm

Hippodrome