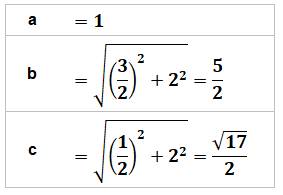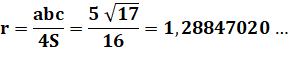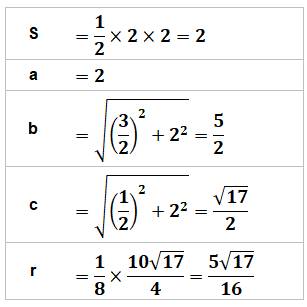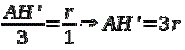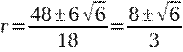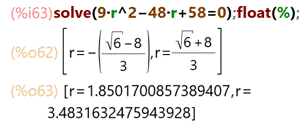|
Édition du: 03/12/2024 |
|
INDEX |
Énigmes en géométrie |
||
|
Exercices 01 |
|||
Faites un double-clic pour un retour en haut de page
![]()
|
CARRÉS dans le CERCLE Résoudre cette
énigme: trois carrés inscrits dans un cercle. Quel est le rayon du cercle ? Et d'autres … |
||
|
|
Sommaire de cette page >>> Trois carrés dans un cercle >>> Cercle dans le coin du carré >>> Deux cercles et un carré dans le triangle |
Débutants Glossaire |
|
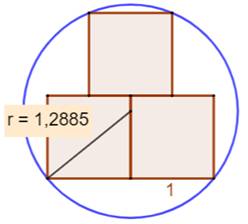
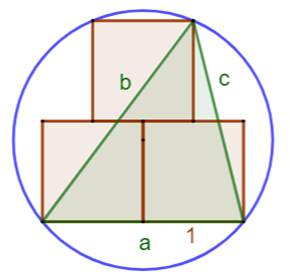
Problème Trois carrés unités, placés comme indiqué. Le cercle circonscrit. Quel est son rayon ? La mesure sur le dessin
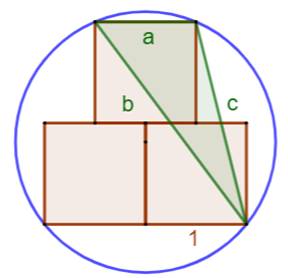
donne 1,2885. Construction et indice On construit le triangle
vert qui est inscrit dans le cercle (les trois sommets sont sur le
cercle). On connait le rayon du
cercle circonscrit à un triangle si on connait la longueur de ses côtés
et son aire. Aire du triangle MNP Le côté MN mesure une unité et sa hauteur en vaut
deux. L'aire est: ½ × 1 × 2 = 1 Longueur des côtés du triangle MNP
Rayon du cercle circonscrit
|
|
|
|
Choix d'un autre triangle inscrit
|
|
|
Simple
application du théorème
de Pythagore et connaissance
de la propriété des segments
de tangente. |
||
|
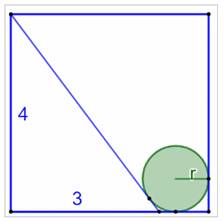
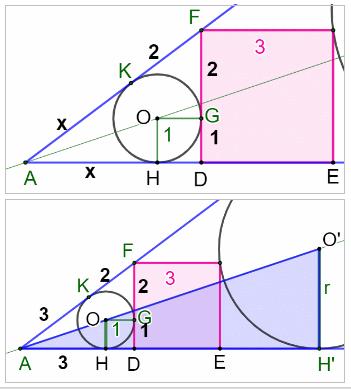
Construction Un
carré de 4 cm de côté et une oblique issue d’un sommet (Voir la figure) .
Elle coupe le côté à 3 cm d’un sommet. On
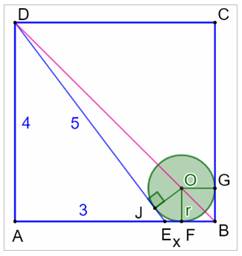
loge un cercle tangent dans le coin du bas. Quel est le rayon du cercle ? Pistes (Voir la figure du bas) Le
triangle rectangle 4, 3 est le célèbre triangle
(3, 4, 5) et DE mesure 5 cm. Le
petit quadrilatère
OGBF est un carré
de côté r. Le segment OB est porté par la diagonale DB à 45°. Le point O est donc situé sur la
diagonale DB et : DB = 4√2 et OB = r√2 Les
segments de tangentes EJ et EF sont égaux (isométriques)
et mesurent 1 – r. (Car EB = 4 – 3 = 1). Dans
le triangle
rectangle DJO, droit en J (point de tangence), le théorème de Pythagore
indique : DO²
= (5 – 1 + r)² + r² = (4√2 –
r√2)² Calculs En
développant : 16
+ 8r + r² + r² = 32 – 16r + 2r² 24r
= 16 r = 2/3 = 0,666... cm |
Figure initiale
Figure avec notations
|
|
|
Simple
application du théorème
de Pythagore et du théorème de
Thalès. |
||
|
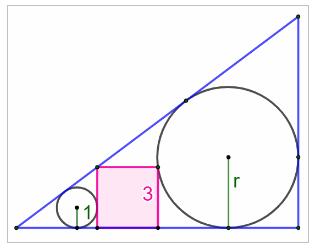
Construction Un
triangle
rectangle contient deux cercles
et un carré
comme l’indique la figure. Quel
est le rayon du grand cercle ? Calcul de x (Voir figures avec notations) Les
segments
de tangentes sont isométriques :
Théorème
de Pythagore dans le triangle rectangle ADF : (x + 2)² = 3² + (x + 1)² Calculs dans le triangle bleu On
a OH = OK = 1 et O est situé sur la bissectrice
de l’angle KAH ; de même pour O’ ; de sorte que A, O et O’ sont
alignés. Les
triangles AHO et AH’O’ sont semblables.
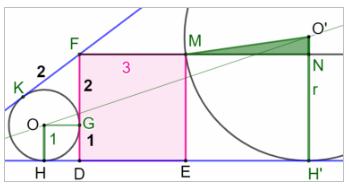
Calculs dans le triangle vert Le segment MN est égal au segment
EH’, lequel vaut : EH’ = AH’ – (3 + 1 + 3) = 3r – 7 Avec le théorème de Pythagore :
Résolution
de l’équation :
Solution r =
1,85017..., r = 3,48316... Or, en observant la construction, il
est évident (on peut facilement le démontrer) que le rayon du grand cercle
est plus grand que le côté du carré ; Seule solution possible : r =
3,48316... Résolution avec Maxima
Voir Maxima / Programmation – Index |
Figure initiale
Figure avec notations
|
|
Haut de page (ou
double-clic)
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
|
|
|
Cette page |
http://villemin.gerard.free.fr/GeomLAV/Triangle/Exercice/CarrCer.htm |