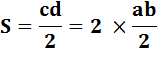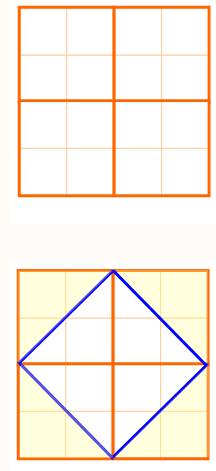
NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 24/10/2014 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique
	CONSTANTES
Débutants Nombres	RACINE de 2 √2 = 1, 41 42 …			Glossaire Nombres
INDEX Puissance Décomposition Général	Introduction	Valeur	Propriétés	Géométrie
	Historique	Calcul	Irrationnel	Doubler
		Sommaire de cette page >>> Dialogue sur la vertu >>> Découverte du dialogue >>> Solution >>> Généralisation

DOUBLER le CARRÉ

Doubler l'aire du carré: pas si évident!

Démarche conduisant à la solution vue par Platon.

Voir la géométrie relative à ce sujet

Doubler l'aire du carré Racine de deux et doubler l'aire du carré

DIALOGUE SUR LA VERTU
Principe Dialogue construit selon un scénario assez classique chez Platon. Trois personnages: Socrate qui affirme qu'il est ignorant; Un tiers, ici, Ménon, laisse entendre qu'il a un certain savoir; Un esclave, utilisé comme faire-valoir. Socrate s'adresse à l'esclave, en présence du tiers. Suit une série de questions: Astucieusement posées, celles-ci dévoilent progressivement la connaissance; Ce qui amène l'esclave comme le tiers à reconnaître qu'ils ne savaient pas grand-chose. Socrate modestement se dit être Celui qui sait qu'il ne sait rien.	Extrait (…) L'ESCLAVE. – Il est évident, Socrate, que cette longueur sera double. SOCRATE. – Tu vois, Ménon, que je ne lui enseigne rien et que je ne fais que le questionner. En ce moment il se figure qu'il sait quelle est la ligne dont doit se former l'espace de huit pieds?. ne crois-tu pas qu'il a cette conviction? MÉNON. – Si. SOCRATE. – Le sait-il donc? MÉNON. – Non certes. SOCRATE. – Il croit qu'il se formerait d'une ligne double? MÉNON. – Oui. (…)

DÉCOUVERTE DU DIALOGUE
Le carré: Deux pieds de côté. Quelle est son aire? S'il y avait un côté de deux pieds et l'autre d'un seul. L'aire serait d'une fois deux pieds. Mais comme le second côté a deux pieds Cela fait deux fois deux pieds; Égal quatre. Un carré double de celui-ci existe Quelle est son aire ? Deux fois quatre; Soit huit. Quelle est la mesure du côté de nouveau carré ? Il est évident que sa longueur sera le double de celle du carré original. Erreur! Premier constat: L'aire sera multipliée par 4 et non par deux! Soit une aire de 16 et non 8 demandé. Deuxième constat: La longueur du côté doit être plus grande que celle du carré de départ (2) et moins grande que celle du carré juste testé (4). Entre 2 et 4, ce doit être 3! Dessinons ce carré de côté égal à trois Quelle est son aire? Trois fois trois égal neuf. Ce n'est pas huit, comme recherché! Solution non trouvée et perplexité de l'auditoire de Socrate.

Extraits condensé du dialogue qui prend place à ce moment là.

SOCRATE. – Alors avec quelle ligne? L'ESCLAVE. – Mais, par Zeus, Socrate, je n'en sais rien. SOCRATE – Remarques-tu, Ménon. Au commencement, il croyait savoir. Il n'avait pas conscience de la difficulté. MÉNON. – Tu dis vrai. SOCRATE. – Il va découvrir avec moi, sans que je fasse autre chose que l'interroger, sans lui rien enseigner.

SOLUTION
Reprenons le dessin déjà vu. Il est constitué de quatre carrés égaux à celui du départ. Son aire est de huit alors que nous cherchons quatre. Il est DEUX fois trop grand. Et si on divisait chaque carré en deux par sa diagonale! L'aire de chacun vaut deux. Il y a quatre tels carrés. L'aire du carré formé (bleu) est égale à quatre fois deux, soit huit, la valeur cherchée.

Généralisation
Pour passer d'une figure à une figure d'aire double, le nombre racine de 2 est souvent impliqué. C'est le cas pour le cercle dont il suffit d'allonger le rayon d'un facteur racine de 2. Dans le cas du triangle rectangle, nous avons: Le théorème de Thales dit que les proportions sont conservées: Quelques calculs: Même principe et même valeur pour doubler le rectangle.

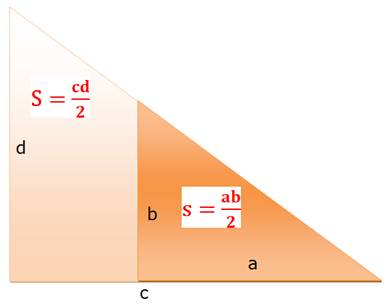
Voir Quadrupler le triangle rectangle

Suite	Historique de racine de deux
Voir	Doubler le volume du cube Constantes Imaginaires Pi Nombre d'Or
DicoNombre	Racine de 2 Racine de 3
Sites	Les dialogues de Platon - Ménon, 80d-86d (texte complet avec dessins) Ménon (texte complet en PDF) Les dialogues de Platon (en général)
Livre	Épistémologie des mathématiques – Jean-Pierre Cléro – Nathan - 1990
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Nombre/Rac2Doub.htm