Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 07/01/2023 M'écrire Brèves de Maths

INDEX Triangle – Général Triangle – Constructions Carré	Quadratures
	Triangles	Parabole	Cercle	Polygone

Quadrature du triangle Il s'agit de transformer un triangle quelconque en un carré de même aire, en utilisant règle et compas seulement. Ces constructions reposent sur la propriété remarquable des triangles rectangles: le carré de la hauteur issue du sommet droit est égal au produit des longueurs découpées sur l'hypoténuse: AH² = HB . HC (relation dite de la moyenne proportionnelle ou moyenne géométrique).
	Sommaire de cette page >>> Triangle quelconque en rectangle >>> Triangle en Carré – Puzzle >>> Quadrature du triangle quelconque >>> Quadrature du triangle rectangle >>> Quadrature du triangle équilatéral >>> Quadrature du rectangle	Débutants Géométrie Glossaire Géométrie

Triangle quelconque en rectangle		haut
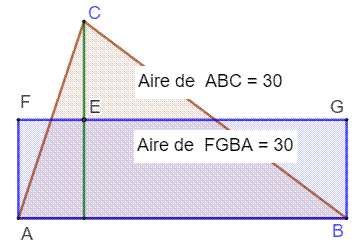
Construction Triangle ABC E est le milieu de la hauteur Rectangle construit sur AB et E. Validation Aire triangle = AC . CE

Voir Constructions élémentaires / Constructions dans les triangles

Triangle en Carré – Puzzle (dissection)		haut
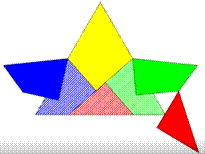
Cette illustration montre comment passer d'un triangle équilatéral à un carré de même aire. La figure colorée montre comment les pièces peuvent être articulées pour passer du triangle au carré par simple rotations.

Voir Dissections

Quadrature du triangle quelconque (1)		haut
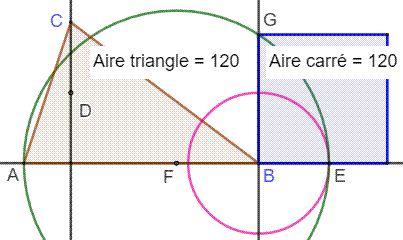
Construction Triangle quelconque ABC. Hauteur issue de C et son milieu D. Perpendiculaire en B à AB. Cercle de centre B et de rayon CD. Intersection avec AB en E. Milieu F de AE pour tracer le cercle vert. Intersection G. BG est le côté du carré.
Démonstration Le triangle AGE est inscrit dans un demi cercle, il est rectangle en G. GB est une des hauteurs de ce triangle Relation métrique avec la hauteur.	GB² = BA.BE = BA.CD Aire du carré = base x demi hauteur de ABC = Aire du triangle

Anglais Rectangle squaring

Quadrature du triangle quelconque (2)		haut
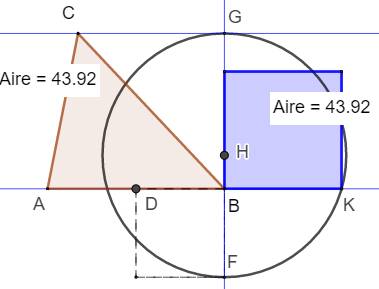
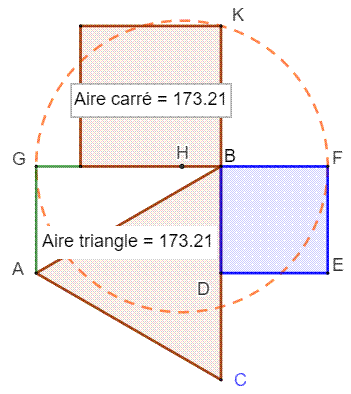
Construction (autre disposition) Triangle équilatéral ABC. D est le milieu de AB. Carré DBF. H est le milieu de FG. Cercle (H, HG). Le triangle GKF est rectangle en K. BK² = BG . BF = AB . h/2 = Aire du triangle. BK est le côté d'un carré de même aire que le triangle ABC.

Cas particuliers

Les méthodes exposées ci-dessus sont valables pour tout type de triangle. Ci-dessous, quelques exemples avec méthodes particulières; toujours basée sur le même principe de la moyenne proportionnelle.

Quadrature du triangle rectangle		haut
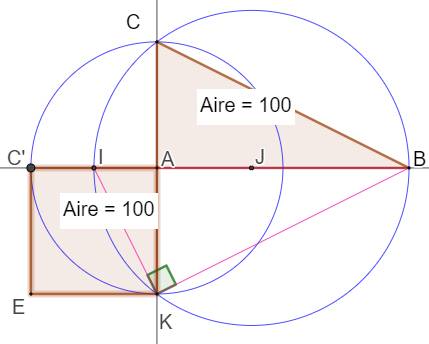
Construction Rectangle ABC. Cercle (A, AC). Intersection avec AB prolongé en C'. I milieu de AC' et J milieu de IB Cercle (J, IJ) Intersection avec AC prolongé en K AK est le côté du carré. Démonstration Triangle IKB inscrit dans un demi-cercle: il est rectangle en K. Relation dans ce triangle: AK² = AB . AI = AB . AC/2 Aire du carré = aire du triangle.

Merci à Patrick Villemin pour cette construction

Quadrature du triangle équilatéral		haut
Construction Triangle équilatéral ABC. D est le milieu de BC. Carré de côté BD. H est le milieu de GF. Cercle (H, GF). Intersection en K avec le prolongement de BC. KB est le côté du carré. Démonstration Du même type que celle présentée ci-dessus: KB² = BG . BF = BC . AD / 2

Quadrature du rectangle		haut
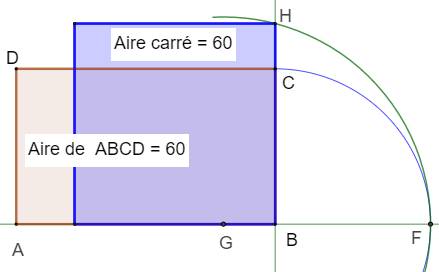
Construction Rectangle ABCD. Report longueur BC sur prolongement de AB: point F. G est le milieu de AF. Report longueur GF sur prolongement de BC: point H BH est le côté du carré Démonstration BH est moyenne géométrique de BA et BF: BH² = AB . BF = AB . BC Aire du carré = aire du rectangle.

Haut de page

Retour	Triangle Carré
Suite	Quadrature du polygone Quadrature du cercle Constructions élémentaires Constructions dans les triangles
Voir	Allumettes Carré – Index Construction à la règle et au compas – Index Dénombrer – Index DicoMot Maths Énigmes classiques Ensembles – les compter Géométrie – Index Jeux – Index Le terrain de basket Losange Rectangles dans le cube Rectangles emboîtés
Sites	Quadrature du triangle – Serge Mehl Quadrature du triangle équilatéral avec GeoGebra La quadrature du triangle – Andrés Navas – CNRS – Façon puzzle (dissection) Triangle squaring – Wolfram MathWorld
Cette page	http://villemin.gerard.free.fr/GeomLAV/Carre/Quadratu.htm