|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
PENTAGONE RÉGULIER – Constructions Impliquant la construction de
bissectrices et autres méthodes Plusieurs
méthodes de construction du pentagone régulier dont celles basées sur la
construction de bissectrices ou celles à
partir de cercles. |
|
|
||
|
Construction de Richmond Réalisation d'un pentagone inscrit dans un cercle
donné. Méthode basée sur l'utilisation des bissectrices Méthode Cercle de
diamètre AB et son diamètre perpendiculaire en D. Intersection
C Le point
milieu P de CD. Droite PB
et intersection S. Bissectrices
(roses): PR de DPB et PQ de DPS Intersections
Q et R. Parallèles
en Q et R à CD. Intersections
F, G, E et H. Pentagone: BEFGH. Note: les Q et R sont les projections sur AB des
sommets du pentagone. |
|
|
|
Justification On retrouve la racine de 5
Théorème des
bissectrices:
|
Angles du pentagone
L'angle UDR vaut 72° caractéristique du pentagone à partir du centre
du cercle circonscrit. Idem pour l'autre côté
L'angle GDQ vaut 36° caractéristique du pentagone à partir du centre
du cercle circonscrit. |
|
Voir Construction par Euclide
utilisant aussi les bissectrices
|
6) Méthode du cercle
tangent |
|
|
|
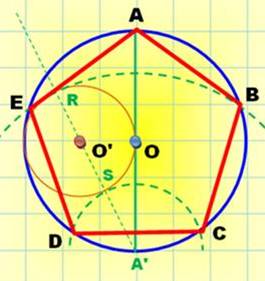
Construction dite du cercle tangent Réalisation d'un pentagone inscrit dans un cercle
donné. Méthode basée sur l'utilisation de deux points de
tangences et de deux droites tangentes Méthode Cercle de
center O; deux diamètres orthogonaux; points AGMN. Point T
milieu du rayon ON Point S
au quart du rayon OG (R est un point de construction, milieu de OG) Cercle
(S, ST) en rose Intersections
P et Q Tangente
au cercle en P et Q Intersections
B, C, D et E Pentagone: ABCDE. |
|
|
|
Justificatif La racine de 5 se cache dans le segment ST
(vert). Or la hauteur du trapèze vaut
rac(5) / 4, soit deux fois ST. D'où la construction avec le cercle rose. |
|
|
|
|
||
|
Construction dite des tangentes Réalisation d'un pentagone inscrit dans un cercle
donné. Méthode basée sur l'utilisation de deux points de
tangences et de deux cercles tangents. Méthode Cercle de
center O. Un point
A sur ce cercle. Diamètre
AO et intersection A'. Point O' milieu du rayon perpendiculaire à AO. Cercle de
centre O' et de rayon OO'. Droite
A'O'. Intersection
en S et R. Cercle de
centre A' et de rayon A'S. Cercle de
centre A' et de rayon A'R. Avec A,
les intersections BCDE forment le pentagone. Pentagone: ABCDE. |
|
|
|
Justification avec OA = OB = R = 1 On montre que l'angle CDH = 36°, caractéristique
du pentagone.
Dans le triangle rectangle CDH (rectangle en H,
car inscrit dans un demi-cercle de diamètre CD):
Arc CH intercepté par les angles alpha et béta: |
|
|
|
Autre justification avec sommets B
et C (et même chose par symétrie pour A et E) |
|
|
Les triangles FQO et FOC sont
semblables En partant du rayon: OF² = FP² – OP² = (FP – OP)(FP + OP) = (FP – PG) (FP + PH) = FG . FH = FQ . FC = le produit des rayons des cercles verts. On écrit OF² = FQ.FC sous cette forme:
Le triangle FOC est isocèle (car OF = OC): Les triangles FQO et FOC sont semblables car: un angle commun en F, et des côtés
proportionnels. Illustration:
|
|
|
Angle au centre O = angle du
pentagone (Pi/5) Semblables, or FOC est isocèle, donc FQO aussi Angles: b
= e = d et a + d = f = 180 – 2b = FOC On devine
que b = e = d = 36° et a + d = f = 108° D'après la construction: GH = QC = R = 1 Avec QC = OC, le triangle COQ est isocèle: |
Nous avons d'un côté FOC = a + d = 180 – 2b Autre évaluation de FOC avec e = b: En rapprochant:
|
|
Le point B est un sommet du pentagone Si le point B est bien un sommet du pentagone on
doit retrouve que l'angle FOB = d = 36°, ce qui est le cas; Et que le triangle FBQ est bien le triangle
isocèle obtenu avec deux rayons (FB et FQ) du cercle vert. |
Dans le triangle FQB: Le triangle FBQ est bien isocèle |
Démonstration inspirée de celle de Patrice Debart – Construire
un pentagone régulier
|
|
||
|
Construction Réalisation d'un pentagone inscrit dans un cercle
donné. Méthode basée sur l'utilisation de deux points de
tangences et de deux cercles tangents. Méthode On
souhaite tracer le pentagone dans le cercle AB (rose). Cercle de
centre B et de rayon AB. Intersection
en C. Droite
BC. Intersection
D. Droite
AD. Intersection
E. Cercle de
centre B de rayon CE (pointillés) Intersection
F. La
longueur du segment EF est celle du pentagone. La
relever au compas et la reporter sur le cercle pour construire le pentagone
comme indiqué ci-dessous. Quelques éléments de calculs
Le calcul de AF est à justifier: Dans le triangle FAB, Angle en A = 120°= 2Pi/3,
AB = R = 1 et FB = rac(2). Loi des sinus:
sin(AFB) = 1.sin(120°) / rac(2) Il faudrait une formulation directe sans passer
par les arcsinus. |
|
|
|
Construction des points du
pentagone Cercle de
centre B et de rayon EF. Intersections
G et H. Cercle de
centre G et de rayon EF. Cercle de
centre H et de rayon EF. Intersections
I et J. Pentagone: BGJIH. |
|
|
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Sites |
Voir les liens en première page
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Geometri/PentaCo2.htm
|
![]()